Soit une courbe quelconque $C$ d’un espace de Riemann $\mathcal {R}_{n}$ définie par une représentation
paramétrique $u^{i}(t)$. Un point $M_{0}$ de la courbe est pris comme origine et correspond à la valeur $t=0$
du paramètre $t$.
Nous nous proposons de faire correspondre, à chaque point $M$ de la courbe $C$, un point $m$ et un repère $(m,\beq {e_{i}})$ de l’espace euclidien $\varepsilon _{n}$. Pour cela, considérons dans l’espace euclidien un point $m_{0}$ de départ auquel nous attachons un repère cartésien $(m_{0},\beq {e^{0}_{i}})$, déterminé en grandeur et en forme, mais pas en orientation, par les valeurs numériques des $g_{ij}$ de l’espace de Riemann au point $M_{0}$ ; on a donc :
\begin{equation}
\beq{e^{0}_{i}}\,\cdot\,\beq{e^{0}_{j}}=(g_{ij})_{0}
\tag{6.5.1}
\label{6.5.1}
\end{equation}
D’autre part, les points $m$ de l’espace euclidien et les vecteurs des repères naturels $(m,\beq {e_{i}})$ vérifient les relations différentielles :
\begin{equation}
\text{d}\beq{m}=\text{d}u^{i}\,\beq{e_{i}}\,\,\,\,;\,\,\,\,\text{d}\beq{e_{i}}=(\sgammaeq{i}{l}{k})_{M}\,\text{d}u^{k}\,\beq{e_{l}}
\tag{6.5.2}
\label{6.5.2}
\end{equation}
où les $(\sgammaeq {i}{l}{k})_{M}$ sont les valeurs des symboles de Christoffel calculés à partir des $g_{ij}$ de la métrique
riemannienne au point $M$ de la courbe $C$. Ce sont donc des fonctions qui dépendent du seul
paramètre $t$.
Les fonctions inconnues $\beq {m}(t)$ et $\beq {e_{k}}(t)$ peuvent être obtenues par intégration du système
différentiel (6.5.2) avec les conditions initiales précédentes pour $t=0$. On obtient alors une
courbe, définie par $\beq {m}(t)$, qui est appelée le développement de la courbe $C$ sur l’espace euclidien.
On notera $\Gamma $ le développement de la courbe $C$.
Métrique euclidienne de raccordement - Plus précisément, on va montrer qu’il
existe dans l’espace euclidien $\varepsilon _{n}$ une métrique telle que que ses coefficients $\gamma _{ij}$ et leurs dérivées
premières, pris le long de la courbe $\beq {m}(t)$, ont les mêmes valeurs numériques que les coefficients
$g_{ij}$et leurs dérivées premières, aux points homologues de la courbe $C$ dans l’espace de
Riemann.
Cela siginifie qu’il existe une métrique euclidienne osculatrice à la métrique
donnée le long de la courbe $C$. On dira que cette métrique euclidienne osculatrice
constitue la métrique euclidienne de raccordement le long de la courbe
$C$.
Détermination d’une métrique euclidienne de raccordement - Soit une courbe $C$ d’un espace de Riemann $\mathcal {R}_{n}$ telle que :
\begin{equation}
u^{2}=u^{3}=...=u^{n}=0
\tag{6.5.3}
\label{6.5.3}
\end{equation}
ce qui ne restreint pas la généralité puisque l’on peut toujours faire un changement
des coordonnées de $\mathcal {R}_{n}$. Les variations de la coordonnée $u^{1}(t)$ dépendent du paramètre
$t$.
Utilisons la convention suivante sur les indices : ceux notés par des lettres grecques prendront les valeurs 2 à $n$, tandis que ceux notés par des lettres latines prendront les valeurs 1 à $n$. Dans ces conditions, le développement $\Gamma $ de la courbe $C$ est une courbe de l’espace euclidien déterminée par les relations différentielles suivantes :
\begin{equation}
(a)\,\,\,\,\text{d}\beq{m}=\text{d}u^{1}\,\beq{e_{1}}\,\,\,\,;\,\,\,\,(b)\,\,\,\,\text{d}\beq{e_{i}}=(\sgammaeq{1}{k}{i})_{u^{\alpha}=0}\,\text{d}u^{1}\,\beq{e_{k}}
\tag{6.5.4}
\label{6.5.4}
\end{equation}
Cherchons à présent un système de coordonnées $u^{i}$ de l’espace euclidien qui donne une métrique euclidienne osculatrice à la métrique riemannienne simultanément en tous les points de $C$. Pour cela, à tout point $P$ de coordonnées $u^{i}$, situé au voisinage d’un point $M$ de $C$, faisons correspondre un point $p$ au voisinage de $m$ dans $\varepsilon _{n}$ en posant :
\begin{equation}
\beq{mp}=u^{\beta}\,\beq{e_{\beta}}+(1/2)\,(\sgammaeq{\beta}{i}{\gamma})_{u^{\alpha}=0}\,u^{\beta}\,u^{\gamma}\,\beq{e_{i}}+\phi^{i}\,(u^{\beta})\,\beq{e_{i}}
\tag{6.5.5}
\label{6.5.5}
\end{equation}
où les fonctions $\phi ^{i}\,(u^{\beta })$ sont du troisième ordre par rapport aux variables $u^{\beta }$. On obtient ainsi un système de coordonnées curvilignes $u^{i}$, dans $\varepsilon _{n}$, qui permet de localiser chaque point $p$ au voisinage de la courbe $C$. Pour un tel système de coordonnées $u^{i}$, le repère naturel au point $m(u^{\alpha }=0)$ est parfaitement défini par les vecteurs donnés par les relations (6.5.4) et (6.5.5), à savoir :
\begin{equation}
\bigg(\dfrac{\partial\,\beq{p}}{\partial\,u^{1}}\bigg)_{u^{\alpha}=0}=\dfrac{\text{d}\beq{m}}{\text{d}u^{1}}=\beq{e_{1}}\,\,\,\,;\,\,\,\,\bigg(\dfrac{\partial\,\beq{p}}{\partial\,u^{\beta}}\bigg)_{u^{\alpha}=0}=\beq{e_{\beta}}
\tag{6.5.6}
\label{6.5.6}
\end{equation}
On obtient ainsi un repère naturel identique à celui qui a été obtenu précédemment
par intégration du système différentiel (6.5.2) lors du développement de la courbe $C$. La
métrique de $\varepsilon _{n}$, dans le système de coordonnées $u^{i}$, admet donc pour coefficients $\gamma _{ij}$ au point $m$ les
produits scalaires $\beq {e_{i}}\,\cdot \,\beq {e_{j}}$.
Montrons que les coefficients $\gamma _{ij}$ sont égaux, en tout point de la courbe $\Gamma $, aux coefficients $g_{ij}$ de la métrique riemannienne. Pour cela, utilisons la relation (6.5.4)(b) dans l’expression de la différentielle du produit scalaire $\beq {e_{i}}\,\cdot \,\beq {e_{j}}$, soit :
\begin{equation}
\text{d}(\beq{e_{i}}\,\cdot\,\beq{e_{j}})=\beq{e_{i}}\,\cdot\,\text{d}\beq{e_{j}}+\beq{e_{j}}\,\cdot\,\text{d}\beq{e_{i}}=(\sgammaeq{i}{l}{k})_{M}\,(\beq{e_{l}}\,\cdot\,\beq{e_{j}})\,\text{d}u^{k}+(\sgammaeq{j}{l}{k})_{M}\,(\beq{e_{l}}\,\cdot\,\beq{e_{i}})\,\text{d}u^{k}
\tag{6.5.7}
\label{6.5.7}
\end{equation}
De leur coté, les coefficients $g_{ij}$ de la métrique riemannienne sont liés aux symboles de Christoffel par la relation (5.1.26), à savoir :
\begin{equation}
\text{d}g_{ij}=\omega_{ij}+\omega_{ji}=(\pgammaeq{ikj}+\pgammaeq{jki})\,\text{d}u^{k}
\tag{6.5.8}
\label{6.5.8}
\end{equation}
Ces coefficients vérifient donc les relations différentielles :
\begin{equation}
\text{d}g_{ij}=(\sgammaeq{i}{l}{k})_{M}\,g_{jl}\,\text{d}u^{k}+(\sgammaeq{j}{l}{k})_{M}\,g_{il}\,\text{d}u^{k}
\tag{6.5.9}
\label{6.5.9}
\end{equation}
La comparaison des relations (6.5.7) et (6.5.9) montrent que les quantités $(\beq {e_{i}}\,\cdot \,\beq {e_{j}})$ et $g_{ij}$ vérifient respectivement un même système différentiel en tout point $M$ de la courbe $C$. Puisqu’on a, au point $M_{0}$, selon (6.5.1), des conditions initiales identiques, à savoir : $\beq {e^{0}_{i}}\,\cdot \,\beq {e^{0}_{j}}=(g_{ij})_{0}$, on obtient en tout point $M$ de $C$ :
\begin{equation}
\beq{e_{i}}\,\cdot\,\beq{e_{j}}=g_{ij}
\tag{6.5.10}
\label{6.5.10}
\end{equation}
Les métriques euclidiennes et riemannienne sont donc tangentes en tous les points de
la courbe $C$. Montrons qu’elles sont également osculatrices le long de cette courbe.
Pour cela, il suffit de démontrer que les valeurs numériques $(\sgammaeq {j}{l}{k})_{M}$ sont également les
valeurs des symboles de Christoffel sur la courbe $\Gamma $ pour la métrique euclidienne.
Les symboles de Christoffel sont les coefficients des vecteurs $\mathbf {e_{k}}$ dans la décomposition du vecteur $\bigg (\dfrac {\partial ^{2}\,\beq {p}}{\partial \,u^{i}\,\partial \,u^{1}}\bigg )$. Or, d’après les relations (6.5.4)(b) et (6.5.6) on a pour la coordonnée $u^{1}$ :
\begin{equation}
\bigg(\dfrac{\partial^{2}\,\beq{p}}{\partial\,u^{i}\,\partial\,u^{1}}\bigg)_{u^{\alpha}=0}=\dfrac{\text{d}\beq{e_{i}}}{\text{d}u^{1}}=(\sgammaeq{1}{k}{i})_{u^{\alpha}=0}\,\beq{e_{k}}
\tag{6.5.11}
\label{6.5.11}
\end{equation}
et pour les autres coordonnées, on obtient d’après la relation (1.5.31) :
\begin{equation}
\bigg(\dfrac{\partial^{2}\,\beq{p}}{\partial\,u^{\beta}\,\partial\,u^{\gamma}}\bigg)_{u^{\alpha}=0}=(\sgammaeq{\beta}{k}{\gamma})_{u^{\alpha}=0}\,\beq{e_{k}}
\tag{6.5.12}
\label{6.5.12}
\end{equation}
La métrique euclidienne est donc osculatrice le long de la courbe $C$ et constitue une
métrique euclidienne de raccordement le long de cette courbe.
Espace euclidien de raccordement - De même que pour les métriques euclidiennes
tangentes ou osculatrices auxquelles on a associé un espace euclidien tangent ou
osculateur, on peut associer à la métrique euclidienne de raccordement un espace
euclidien de raccordement.
Grâce à la détermination, en chaque point $m$, d’un repère cartésien, on a en réalité développé sur l’espace euclidien non seulement la courbe donnée mais encore toute la région infiniment petite de l’espace de Riemann qui entoure cette courbe. La relation (1.5.31) définit les coordonnées curvilignes de cet espace euclidien de raccordement.
Le développement d’une courbe et l’utilisation d’une métrique euclidienne de
raccordement permettent de mettre en évidence diverses propriétés géométriques des
espaces de Riemann. Étudions auparavant des exemples de transport parallèle le long
d’une courbe.
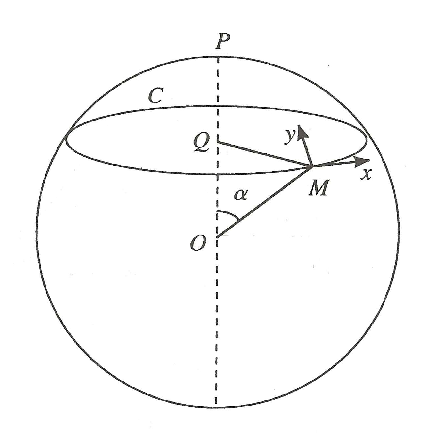
Déplacement le long d’un petit cercle d’une sphère - On a une représentation
concrète d’un espace de raccordement le long d’une courbe $C$ en projetant orthogonalement
les points d’une surface de Riemann sur la développable $S$ circonscrite à la surface le long
de la courbe $C$. Dans ce cas, les métriques des deux surfaces sont osculatrices en chaque
point de $C$ et d’autre part, la métrique de $S$ est euclidienne. Par suite, la surface $S$ déroulée
sur un plan, donne un espace euclidien de raccordement le long de la courbe
$C$.
On a vu qu’une surface sphérique à deux dimensions constitue un espace de Riemann.
Considérons sur une sphère de rayon $R$, un petit cercle $C$ de pôle $P$. Soit $\alpha $ le demi-angle au
sommet du cône qui a pour sommet le centre $O$ de la sphère et pour base le petit cercle $C$
(Fig.6.2).
Dans le cas de la sphère considérée, le développement du cercle $C$ sur un plan s’obtient
en développant la développable circonscrite à la sphère le long du cercle. Cette
développable est un cône dont les génératrices ont pour longueur $R\,\text {tan}\,\alpha $. La surface du cône,
déroulé sur un plan, fournit un espace euclidien (Fig.6.3).
Le développement de la courbe $C$ donne un arc de cercle, de centre $Q$ et de rayon $R$ ; la
longueur de cet arc de cercle est celle du petit cercle de la sphère, à savoir $2\pi R\,\text {sin}\,\alpha $. On voit
que le point de départ $m$ dans l’espace euclidien ne coïncide pas avec le point
d’arrivée $m'$, après avoir parcouru le cycle formé dans le cas présent par le cercle
$C$.
Si $\Phi $ désigne l’angle $m'Qm$, on a :
\begin{equation}
(R\,\text{tan}\,\alpha)\,(2\pi-\Phi)=2\pi\,R\,\text{sin}\,\alpha
\tag{6.5.15}
\label{6.5.15}
\end{equation}
D’autre part, l’aire limitée sur la sphère par le petit cercle, est en coordonnées sphériques :
\begin{equation}
\mathlarger{\int}_{0}^{2\pi}\,\mathlarger{\int}_{0}^{\alpha}\,R^{2}\,\text{sin}\,\theta\,\text{d}\theta\,\text{d}\varphi=2\pi\,R^{2}\,(1-\text{cos}\,\alpha)
\tag{6.5.16}
\label{6.5.16}
\end{equation}
On obtient la relation suivante entre l’aire $S$ déterminée par le cycle, ici la courbe $C$, et le carré du rayon de courbure de la surface considérée, ici la sphère de rayon $R$ :
\begin{equation}
\Phi=S/R^{2}
\tag{6.5.17}
\label{6.5.17}
\end{equation}
Attachons à chaque point $M$ du cercle deux axes rectangulaires, $Mx$ tangent au
cercle dans le sens du parcours choisi, $My$ tangent à la méridienne passant par $M$.
Ces axes occupent les positions représentées sur la figure 6.2. Effectuons un
transport parallèle des vecteurs portés par ces axes. Dans l’espace euclidien
de raccordement, ces axes ont les positions $mx$ et $my$ au début du parcours, et les
positions $m'x'$ et $m'y'$ en fin de parcours du cercle (Fig.6.3). Pour retrouver la position
initiale, il faut, dans l’espace euclidien, effectuer un déplacement associé formé
par :
\begin{equation}
2\,R\,\text{tan}\,\alpha\,\text{sin}(\Phi/2)
\tag{6.5.18}
\end{equation}
Déplacement le long d’un triangle sphérique - Retrouvons par un calcul de
géométrie sphérique les mêmes propriétés que ci-dessus mais pour un cycle
différent.
Considérons un triangle sphérique $M_{0}M_{1}M_{2}$ formé par les intersections de trois géodésiques.
Appelons $a_{0}, a_{1}, a_{2}$, les valeurs des angles respectifs des tangentes aux géodésiques aux points $M_{0}, M_{1}, M_{2}$.
Soit un vecteur $\mathbf {v}$ qui au point $M_{0}$ fait un angle $\alpha $ avec la tangente en ce point à la géodésique
allant de $M_{0}$ à $M_{1}$ (Fig.6.4).
Réalisons un transport parallèle du vecteur $\mathbf {v}$ le long de $M_{0}M_{1}$. Appelons $\mathbf {v_{1}}$ le vecteur $\mathbf {v}$ lorsqu’il
est transporté parallèlement au point $M_{1}$ ; les vecteurs $\mathbf {v}$ et $\mathbf {v_{1}}$ sont équipollents par
rapport à la géodésique $M_{0}M_{1}$. En $M_{1}$, le vecteur $\mathbf {v_{1}}$ fait avec la tangente $M_{1}M_{2}$ un angle égal à
$\beta =(\pi -a_{1}-\alpha )$.
Transportons parallèlement le vecteur $\mathbf {v_{1}}$ le long de la géodésique $M_{1}M_{2}$ ; on obtient le vecteur $\mathbf {v_{2}}$ équipollent à $\mathbf {v_{1}}$ au point $M_{2}$. Puis on effectue un transport parallèle de $\mathbf {v_{2}}$ le long de $M_{2}M_{0}$ et l’on obtient $\mathbf {v_{3}}$ au point $M_{0}$. Finalement, après un transport parallèle selon ce circuit fermé, le vecteur initial $\mathbf {v}$ a tourné d’un angle $\epsilon $ tel que :
\begin{equation}
\epsilon=a_{0}+a_{1}+a_{2}-\pi
\tag{6.5.20}
\label{6.5.20}
\end{equation}
L’angle $\epsilon $ est appelé excès sphérique du triangle. cette quantité, nulle pour un
triangle plan, est positive pour un triangle sphérique. On démontre que l’aire du triangle
sphérique, pour une sphère de rayon $R$, est égale à $R^{2}\,\epsilon $. On retrouve l’expression (6.5.17)
donnant la relation entre l’angle de rotation du vecteur transporté et l’aire de la surface
délimitée par le circuit parcouru.
Déplacement associé - La propriété de rotation d’un vecteur transporté
parallèlement le long d’un cycle se généralise pour une surface quelconque.
De manière générale, si l’on considère dans un espace de Riemann, un cycle
partant d’un point $M_{0}$, on va développer ce cycle dans l’espace euclidien en partant
de $m_{0}$ et du repère $(m_{0},\beq {e_{i}})$, on obtient, après avoir transporté parallèlement le repère
le long du cycle, une position finale $m'_{0}$ et un repère $(m'_{0},\beq {e'_{i}})$. Pour retrouver la position
initiale, dans l’espace euclidien, il faudra effectuer un certain déplacement qui
amène le point $m'_{0}$ en $m_{0}$ et le repère $(m'_{0},\beq {e'_{i}})$ en $(m_{0},\beq {e_{i}})$. Ce déplacement est dit associé au cycle
considéré.
Le déplacement associé à un cycle peut être déterminé d’une façon équivalente en considérant deux chemins différents le long de ce cycle. Considérons un cycle $M_{0}\,C\,M_{1}\,C'\,M_{0}$ (Fig.6.5) d’un espace de Riemann et partons du point intermédiaire $M_{1}$ pour aller vers $M_{0}$ selon deux chemins différents $M_{1}\,C\,M_{0}$ et $M_{1}\,C'\,M_{0}$. Le développement de ces deux chemins sur l’espace euclidien de raccordement donne des repères dont les positions finales, en $M_{0}$, sont distinctes. Le déplacement qui amène ces deux repères à coïncider est identique au déplacement associé au cycle.
Le calcul du déplacement associé à un cycle élémentaire va nous permettre d’exprimer la
rotation subie par un vecteur après un transport par équipollence le long d’un cycle. La
méthode suivante a été imaginée par Elie Cartan.
Pour cela, considérons deux systèmes de différentiation désignés respectivement par les symboles $\text {d}$ et $\delta $. Soit un point $M$ quelconque, de coordonnées $u^{i}$, d’un espace de Riemann ; soit $M_{1}$ le point de coordonnées $(u^{i}+d\,u^{i})$ et $M_{2}$ le point de coordonnées $(u^{i}+\delta \,u^{i})$. Le vecteur $\mathbf {MM_{1}}$ définit un déplacement élémentaire $\beq {\text {d}_{1}}$ ; le vecteur $MM_{2}$, un déplacement élément élémentaire $\beq {\text {d}_{2}}$. Effectuons à présent sur le point $M_{1}$, un déplacement élémentaire $\beq {\text {d}_{2}}$, on obtient un point $M_{3}$ de coordonnées :
\begin{equation}
u^{i}+\text{d}u^{i}+\delta\,(u^{i}+\text{d}u^{i})=u^{i}+\text{d}u^{i}+\delta\,u^{i}+\delta\,\text{d}u^{i}
\tag{6.5.22}
\label{6.5.22}
\end{equation}
Effectuons de même sur $M_{2}$, le déplacement élémentaire $\beq {\text {d}_{1}}$ ; on obtient un point $M'_{3}$ de coordonnées :
\begin{equation}
u^{i}+\delta\,u^{i}+\text{d}(u^{i}+\delta\,u^{i})=u^{i}+\delta\,u^{i}+\text{d}u^{i}+\text{d}\delta\,u^{i}
\tag{6.5.23}
\label{6.5.23}
\end{equation}
On voit que le point $M'_{3}$ coïncidera avec le point $M_{3}$ si l’on a :
\begin{equation}
\text{d}\delta\,u^{i}=\delta\,\text{d}u^{i}
\tag{6.5.24}
\label{6.5.24}
\end{equation}
autrement dit les deux différentiations sont interchangeables. Dans ce cas, si $f(u^{i})$ est une fonction deux fois continuement dérivable des variables $u^{i}$, on a :
\begin{equation}
\delta\,f=\partial_{i}\,f\,\delta\,u^{i}\,\,\,\,\text{et}\,\,\,\,\text{d}\delta\,f=\partial_{ij}\,f\,\delta\,u^{i}\,\text{d}u^{j}+\partial_{i}\,f\,\text{d}\delta\,u^{i}
\tag{6.5.25}
\label{6.5.25}
\end{equation}
Un même calcul pour $\delta \,\text {d}f$ nous donne, en admettant l’égalité (6.5.24) :
\begin{equation}
\text{d}\delta\,f=\delta\,\text{d}f
\tag{6.5.26}
\label{6.5.26}
\end{equation}
Nous supposerons par la suite que les deux différentiations considérées sont échangeables entre elles. Considérons alors un cycle élémentaire $M\,M_{1}\,M_{3}\,M_{2}\,M$ d’un espace riemannien, formé de quatre cotés (Fig.6.6) constituant un quasi-parallélogramme. Nous supposerons que ce cycle est parcouru dans l’odre indiqué par la notation.
Développons les deux chemins qui du point $M$ vont au point $M_{3}$, l’un étant $M\,M_{1}\,M_{3}$ et l’autre $M\,M_{2}\,M_{3}$. Développons d’abord sur l’espace euclidien le côté $M\,M_{1}$ du cycle. Au point $M$ correspond un repère euclidien $(m,\beq {e_{i}})$ ; lorsqu’on passe au point infiniment voisin $M_{1}$, on a les variations élémentaires suivantes :
\begin{equation}
\text{d}\beq{m}=\text{d}u^{k}\,\beq{e_{k}}\,\,\,\,;\,\,\,\,\text{d}\beq{e_{i}}=\mixescomponents{k}{i}(\text{d})\,\beq{e_{k}}
\tag{6.5.28}
\label{6.5.28}
\end{equation}
où $\omega ^{k}_{i}(d)$ désigne la forme différentielle prise pour les $\text {d}u^{k}$.
De même, le développement de $M\,M_{2}$ donne les variations :
\begin{equation}
\delta\,\beq{m}=\delta\,u^{k}\,\beq{e_{k}}\,\,\,\,;\,\,\,\,\delta\,\beq{e_{i}}=\mixescomponents{k}{i}(\delta)\,\beq{e_{k}}
\tag{6.5.29}
\label{6.5.29}
\end{equation}
Le développement du chemin $M_{1}\,M_{3}$ va se faire en partant, dans l’espace euclidien, du point $m_{1}$ et du repère $(m_{1},(\beq {e_{i}})_{1})$. Pour cela, il faut appliquer l’opération $\delta $ définie par les formules (6.5.29) mais au lieu de considérer les coordonnées $u^{i}$ il faut à présent les remplacer par $u^{i}+\text {d}u^{i}$, puisqu’on part du point $M_{1}$. On obtient, dans l’espace euclidien, un point d’arrivée $m_{3}$ et un repère $(m_{3},(\beq {e_{i}})_{3})$ tels que :
\begin{align}
\beq{mm_{3}} &= \text{d}\beq{m}+\delta(\beq{m}+\text{d}\beq{m}) = \text{d}\beq{m}+\delta\,\beq{m}+\delta\,\text{d}\beq{m} \notag \\
(\beq{e_{i}})_{3} &= \beq{e_{i}}+\text{d}\beq{e_{i}}+\delta(\beq{e_{i}}+\text{d}\beq{e_{i}})
\tag{6.5.30}
\label{6.5.30}
\end{align}
Le développement du chemin $M\,M_{2}\,M_{3}$ nous donne un point d’arrivée $m'_{3}$ et un repère en ce point $(m'_{3},(\beq {e'_{i}})_{3})$ tels que :
\begin{align}
\beq{mm’_{3}} &= \delta\,\beq{m}+\text{d}(\beq{m}+\delta\,\beq{m}) = \delta\,\beq{m}+\text{d}\beq{m}+\text{d}\delta\,\beq{m} \notag \\
(\beq{e_{i}})_{3} &= \beq{e_{i}}+\text{d}\beq{e_{i}}+\delta(\beq{e_{i}}+\text{d}\beq{e_{i}})
\tag{6.5.31}
\label{6.5.31}
\end{align}
Par suite, pour passer du repère $(m_{3},(\beq {e_{i}})_{3})$ au repère $(m'_{3},(\beq {e'_{i}})_{3})$, il faut effectuer un déplacement donné par les formules :
\begin{align}
\beq{mm’_{3}}-\beq{mm_{3}} &= \text{d}\delta\,\beq{m}-\delta\,\text{d}\beq{m}
\tag{6.5.32}
\label{6.5.32} \\
(\beq{e’_{i}})_{3}-(\beq{e_{i}})_{3} &= \text{d}\delta\,\beq{e_{i}}-\delta\,\text{d}\beq{e_{i}}
\tag{6.5.33}
\label{6.5.33}
\end{align}
Calculons l’expression du second membre de (6.5.32) à l’aide des relations (6.5.28) et (6.5.29), on obtient :
\begin{align}
\text{d}\delta\,\beq{m}-\delta\,\text{d}\beq{m} &= \text{d}\delta\,u^{k}\,\beq{e_{k}}-\delta\,\text{d}u^{k}\,\beq{e_{k}} = \delta\,u^{k}\,\text{d}\beq{e_{k}}-\text{d}u^{k}\,\delta\,\beq{e_{k}} \notag \\
&= [\delta\,u^{k}\,\mixescomponents{i}{k}(\text{d})-\text{d}u^{k}\,\mixescomponents{i}{k}(\delta)]\,\beq{e_{i}} = [\sgammaeq{s}{i}{r}-\sgammaeq{r}{i}{s}]\,\text{d}u^{r}\,\delta\,u^{s}\,\beq{e_{i}}=0
\tag{6.5.34}
\label{6.5.34}
\end{align}
Les deux développements conduisent, à l’approximation considérée, au même point $m_{3}$ pour le repère final. Comparons à présent les vecteurs des deux repères qui ont transité par deux chemins différents. On a :
\begin{align}
\text{d}\delta\,\beq{e_{i}}-\delta\,\text{d}\beq{e_{i}} &= \text{d}[\mixescomponents{k}{i}(\delta)\beq{e_{k}}-\delta\,\mixescomponents{k}{i}(\text{d})\beq{e_{k}}] \notag \\
&= [\text{d}\mixescomponents{j}{i}(\delta)-\delta\,\mixescomponents{j}{i}(\text{d})]\,\beq{e_{j}}+\mixescomponents{k}{i}(\delta)\,\text{d}\beq{e_{k}}-\mixescomponents{k}{i}(\text{d})\,\delta\,\beq{e_{k}}
\tag{6.5.35}
\label{6.5.35}
\end{align}
Les relations (6.5.28) et (6.5.29) nous donnent :
\begin{align}
\text{d}\delta\,\beq{e_{i}}-\delta\,\text{d}\beq{e_{i}} &= [\text{d}\mixescomponents{j}{i}(\delta)-\delta\,\mixescomponents{j}{i}(\text{d})+\mixescomponents{k}{i}(\delta)\,\mixescomponents{j}{k}(\text{d})-\mixescomponents{k}{i}(\text{d})\,\mixescomponents{j}{k}(\delta)]\,\beq{e_{j}}
\tag{6.5.36}
\label{6.5.36}
\end{align}
Posons :
\begin{align}
\Omega^{j}_{i}=\text{d}\mixescomponents{j}{i}(\delta)-\delta\,\mixescomponents{j}{i}(\text{d})+\mixescomponents{k}{i}(\delta)\,\mixescomponents{j}{k}(\text{d})-\mixescomponents{k}{i}(\text{d})\,\mixescomponents{j}{k}(\delta)
\tag{6.5.37}
\label{6.5.37}
\end{align}
Le déplacement associé au cycle élémentaire considéré est alors donné par :
\begin{align}
\text{d}\delta\,\beq{e_{i}}-\delta\,\text{d}\beq{e_{i}}=\Omega^{j}_{i}\,\beq{e_{j}}
\tag{6.5.38}
\label{6.5.38}
\end{align}
Les repères $(m_{3},(\beq {e_{i}})_{3})$ et $(m'_{3},(\beq {e'_{i}})_{3})$ associés aux deux développements ont des orientations différentes
mais ils ont même forme et même grandeur puisque les produits scalaires deux à deux des
vecteurs de ces repères sont donnés par les valeurs en $M_{3}$ des coefficients $g_{ij}$ de la métrique
riemannienne. Par suite, les quantités $\Omega ^{j}_{i}$ définissent une rotation qui fait passer d’un repère
à l’autre.
En conclusion, on voit qu’un déplacement associé à un cycle élémentaire laisse fixe
l’origine du cycle et se réduit donc à une rotation autour de ce point.
Tenseur de rotation - Montrons que les quantités $\Omega ^{j}_{i}$ sont les composantes d’un tenseur. Pour cela, utilisons le changement de base du repère naturel :
\begin{align}
\beq{e_{i}}=A’^{j}_{i}\,\beq{e’_{j}}
\tag{6.5.39}
\label{6.5.39}
\end{align}
d’où :
\begin{align}
\text{d}\beq{e_{i}}=A’^{j}_{i}\,\text{d}\beq{e’_{j}}+(\text{d}A’^{j}_{i})\,\beq{e’_{j}}
\tag{6.5.40}
\label{6.5.40}
\end{align}
Appliquons à la relation précédente le symbole de différentiation $\delta $, il vient :
\begin{align}
\delta\,\text{d}\beq{e_{i}}=A’^{j}_{i}\,\delta\,\text{d}\beq{e’_{j}}+(\delta\,A’^{j}_{i})\,\text{d}\beq{e’_{j}}+(\delta\,\text{d}A’^{j}_{i})\,\beq{e’_{j}}+(\text{d}A’^{j}_{i})\,\delta\,\beq{e’_{j}}
\tag{6.5.41}
\label{6.5.41}
\end{align}
Échangeant l’ordre de différentiation et soustrayant membre à membre, en remarquant que l’on a : $\delta \,\text {d}A'^{j}_{i}=\text {d}\delta \,A'^{j}_{i}$, on obtient la différence géométrique des vecteurs :
\begin{align}
\text{d}\delta\,\beq{e_{i}}-\delta\,\text{d}\beq{e_{i}}=A’^{j}_{i}\,(\text{d}\delta\,\beq{e’_{j}}-\delta\,\text{d}\beq{e’_{j}})
\tag{6.5.42}
\label{6.5.42}
\end{align}
Les quantités $(\text {d}\delta \,\beq {e'_{j}}-\delta \,\text {d}\beq {e'_{j}})$ sont les déplacements géométriques des nouveaux vecteurs $\mathbf {e'_{j}}$ et ces déplacements sont de la forme :
\begin{align}
\text{d}\delta\,\beq{e’_{j}}-\delta\,\text{d}\beq{e’_{j}}=\Omega’^{k}_{j}\,\beq{e’_{k}}
\tag{6.5.43}
\label{6.5.43}
\end{align}
Les relations (6.5.41) et (6.5.42) nous donnent, compte tenu de l’expression (6.5.38) :
\begin{align}
\Omega^{l}_{i}\,\beq{e_{l}}=A’^{j}_{i}\,\Omega’^{k}_{j}\,\beq{e’_{k}}=A’^{j}_{i}\,\Omega’^{k}_{j}\,A^{l}_{k}\,\beq{e_{l}}
\tag{6.5.44}
\label{6.5.44}
\end{align}
Par identification des coefficients des vecteurs $\mathbf {e_{l}}$ dans les deux membres de cette dernière relation, il vient :
\begin{align}
\Omega^{l}_{i}=A’^{j}_{i}\,A^{l}_{k}\,\Omega’^{k}_{j}
\tag{6.5.45}
\label{6.5.45}
\end{align}
ce qui montre que les quantités $\Omega ^{l}_{i}$ sont les composants mixtes d’un tenseur du second ordre.