Exercices resolus

3.8 Exercices résolus

Exercice 3.1

Soit {$\mathbf {e_{1}}$,$\mathbf {e_{2}}$} une base d’un espace vectoriel $E_{2}$ et soient deux vecteurs de $E_{2}$ :

\begin{equation*} \beq{X}=2\,\beq{e_{1}}+4\,\beq{e_{2}}\,\,\,\,;\,\,\,\,\beq{Y}=5\,\beq{e_{1}}+3\,\beq{e_{2}}
\tag{3.8.1} \end{equation*}

1.

On note $\beq {e_{i}}\,\otimes \,\beq {e_{j}}$ les vecteurs de base d’un espace $E_{4}=E_{2}\,\otimes \,E_{2}$. Déterminer l’expression du produit tensoriel $\beq {X}\,\otimes \,\beq {y}$.

2.

Le tenseur suivant :

\begin{equation*} \beq{U}=11\,\beq{e_{1}}\,\otimes\,\beq{e_{1}}+8\,\beq{e_{1}}\,\otimes\,\beq{e_{2}}+20\,\beq{e_{2}}\,\otimes\,\beq{e_{1}}+12\,\beq{e_{2}}\,\otimes\,\beq{e_{2}}
\tag{3.8.2} \end{equation*}

est-il le produit tensoriel de deux vecteurs de $E_{2}$ ?

3.

Montrer que le tenseur $\mathbf {U}$ est la somme du produit tensoriel $\beq {X}\,\otimes \,\beq {Y}$ et d’un autre tenseur $\mathbf {W}$ que l’on déterminera. Ce dernier est-il un produit tensoriel et lequel ?

Solutions

1.

La propriété de distributivité du produit tensoriel par rapport à l’addition vectorielle nous donne :

\begin{equation*} \beq{X}\,\otimes\,\beq{Y}=(2\,\beq{e_{1}}+4\,\beq{e_{2}})\,\otimes\,(5\,\beq{e_{1}}+3\,\beq{e_{2}})
\tag{3.8.3} \end{equation*}

\begin{equation*} =2\,\beq{e_{1}}\,\otimes\,5\,\beq{e_{1}}+2\,\beq{e_{1}}\,\otimes\,3\,\beq{e_{2}}+4\,\beq{e_{2}}\,\otimes\,5\,\beq{e_{1}}+4\,\beq{e_{2}}\,\otimes\,3\,\beq{e_{2}}
\tag{3.8.4} \end{equation*}

L’associativité du produit tensoriel par rapport à la multiplication par un scalaire nous donne :

\begin{equation*} \beq{X}\,\otimes\,\beq{Y}=10\,\beq{e_{1}}\,\otimes\,\beq{e_{1}}+6\,\beq{e_{1}}\,\otimes\,\beq{e_{2}}+20\,\beq{e_{2}}\,\otimes\,\beq{e_{1}}+12\,\beq{e_{2}}\,\otimes\,\beq{e_{2}}
\tag{3.8.5} \end{equation*}

2.

Notons $\mathbf {U}$ le tenseur donné :

Développons cette expression et identifions au tenseur $\mathbf {U}$ donné ; il vient pour les composantes :

\begin{equation*} x^{1}\,y^{1}=11\,\,\,\,;\,\,\,\,x^{1}\,y^{2}=8\,\,\,\,;\,\,\,\,x^{2}\,y^{1}=20\,\,\,\,;\,\,\,\,x^{2}\,y^{2}=12
\tag{3.8.7} \end{equation*}

Le rapport entre les composantes nous donne : $\dfrac {y^{1}}{y^{2}}=\dfrac {11}{8}$ et $\dfrac {y^{1}}{y^{2}}=\dfrac {20}{12}$

Ces valeurs étant différentes, le tenseur $\mathbf {U}$ ne peut pas être le produit tensoriel de deux vecteurs.

3.

Le tenseur $\mathbf {W}$ est égal à : $\beq {W}=\beq {U}-\beq {X}\,\otimes \,\beq {Y}$, d’où : $\beq {W}=\beq {e_{1}}\,\otimes \,\beq {e_{1}}+2\,\beq {e_{1}}\,\otimes \,\beq {e_{2}}$.

Si l’on cherche $\mathbf {W}$ sous forme d’un produit tensoriel, $\beq {W}=v^{i}\,u^{j}\,\beq {e_{i}}\,\otimes \,\beq {e_{j}}$, on obtient par identification :

\begin{equation*} v^{1}\,u^{1}=1\,\,\,\,;\,\,\,\,v^{1}\,u^{2}=2\,\,\,\,;\,\,\,\,v^{2}\,u^{1}=0\,\,\,\,;\,\,\,\,v^{2}\,u^{2}=0
\tag{3.8.8} \end{equation*}

Puisque $u^{1}$ et $u^{2}$ ne peuvent être nuls, selon les premières égalités, on a $v^{2}$=0. Il reste deux équations pour trois inconnues, d’où une certaine indétermination. Prenons $v^{1}=1$, d’où $u^{1}=1$ et $u^{2}=2$ ; on obtient ainsi le produit tensoriel :

\begin{equation*} \beq{W}=\beq{e_{1}}\,\otimes\,(\beq{e_{1}}+2\,\beq{e_{2}})
\tag{3.8.9} \end{equation*}

Exercice 3.2

Les composantes mixtes $t^{i}_{jk}$ d’un tenseur $\mathbf {T}$, appartenant à l’espace produit tensoriel $E^{(3)}_{2}$, sont les suivantes :

\begin{equation*} t^{1}_{11}=0\,\,,\,\,t^{1}_{12}=2\,\,,\,\,t^{1}_{21}=-1\,\,,\,\,t^{1}_{22}=3\,\,,\,\,t^{2}_{11}=1\,\,,\,\,t^{2}_{12}=-1\,\,,\,\,t^{2}_{21}=0\,\,,\,\,t^{2}_{22}=-2
\tag{3.8.10} \end{equation*}

1.

Calculer les composantes contractées $u_{k}=t^{i}_{ik}$ du tenseur $\mathbf {T}$. Écrire l’expression du tenseur $\mathbf {U}$ de composantes $u_{k}$.

2.

On se donne une base {$\mathbf {e_{i}}$} de $E_{2}$ dans laquelle le tenseur fondamental $g_{ij}$ a pour matrice :

\begin{equation*} [g_{ij}]=\begin{bmatrix}
g_{11}&g_{12} \\
g_{21}&g_{22}
\end{bmatrix}=\begin{bmatrix}
2&-3 \\
-3&1
\end{bmatrix}
\tag{3.8.11} \end{equation*}

Déterminer les composantes covariantes $t_{ijk}$ du tenseur $\mathbf {T}$.

3.

Déterminer les composantes contravariantes $g^{ij}$ du tenseur fondamental.

4.

Calculer les composantes mixtes $t^{ij}_{k}$ du tenseur $\mathbf {T}$.

Solutions

1.

Les composantes contractées sont : $u_{k}=t^{i}_{ik}=t^{1}_{1k}+t^{2}_{2k}$ soit :

\begin{equation*} u_{1}=t^{1}_{11}+t^{2}_{21}=0\,\,\,\,;\,\,\,\,u_{2}=t^{1}_{12}+t^{2}_{22}=0
\tag{3.8.12} \end{equation*}

Le tenseur $\mathbf {U}$ de composantes $u_{k}$ est le vecteur nul : $\beq {U}=\beq {0}$.

2.

Les composantes covariantes sont : $t_{ijk}=g_{li}\,t^{l}_{jk}$, d’où :

\begin{equation*} t_{111}=g_{11}\,t^{1}_{11}+g_{21}\,t^{2}_{11}=-3\,\,\,\,;\,\,\,\,t_{112}=7\,\,\,\,;\,\,\,\,t_{121}=-2\,\,\,\,;\,\,\,\,t_{122}=12\,\,\,\,;\,\,\,\,t_{211}=1
\tag{3.8.13} \end{equation*}

\begin{equation*} t_{212}=-7\,\,\,\,;\,\,\,\,t_{221}=3\,\,\,\,;\,\,\,\,t_{222}=-11
\tag{3.8.14} \end{equation*}

3.

Calcul des composantes contravariantes $g^{ij}$ du tenseur fondamental. La formule (1.5.45) nous donne :

\begin{equation*} g_{ik}\,g^{kj}=\delta_{ij}\,\,\,\,\text{avec}\,\,\,\,g^{ij}=g^{ji}
\tag{3.8.15} \end{equation*}

On obtient trois équations qui nous donnent :

\begin{equation*} g^{11}=-\dfrac{1}{7}\,\,\,;\,\,\,g^{21}=g^{12}=-\dfrac{3}{7}\,\,\,;\,\,\,g^{22}=-\dfrac{2}{7}
\tag{3.8.16} \end{equation*}

4.

Les composantes mixtes $t^{ij}_{k}$ du tenseur $\mathbf {T}$ ont pour expression :

\begin{equation*} t^{ij}_{k}=g^{lj}\,t^{i}_{lk}
\tag{3.8.17} \end{equation*}

d’où :

\begin{equation*} t^{11}_{1}=g^{11}\,t^{1}_{11}+g^{21}\,t^{1}_{21}=\dfrac{3}{7}\,\,\,\,;\,\,\,\,t^{11}_{2}=-\dfrac{11}{7}\,\,\,\,;\,\,\,\,t^{12}_{1}=\dfrac{2}{7}\,\,\,;\text{etc}.
\tag{3.8.18} \end{equation*}

Exercice 3.3

En utilisant le critère général de tensorialité, montrer que, pour $i,j=1$ à $n$ :

1.: Les $n^{2}$ quantités $g_{ij}=\beq {e_{i}}\,\cdot \,\beq {e_{j}}$ constituent les composantes covariantes d’un tenseur.
2.: Les $n^{2}$ quantités $\delta _{i}^{j}$ constituent les composantes mixtes d’un tenseur.

Solutions

1.

Formons le produit tensoriel des quantités $g_{ij}$ avec les composantes contravariantes $v^{k}$ d’un tenseur $\mathbf {V}$ d’ordre un ; on obtient :

\begin{equation*} g_{ij}\,v^{k}\,\,\,\,;\,\,\,\,i,j,k=1,...,n
\tag{3.8.19} \end{equation*}

La contraction sur les indices $j$ et $k$ nous donne l’expression des composantes covariantes du tenseur $\mathbf {V}$, soit :

\begin{equation*} g_{ij}\,v^{j}=v_{i}
\tag{3.8.20} \end{equation*}

On obtient ainsi un tenseur d’ordre un et, selon le critère général de tensorialité, les $g_{ij}$sont donc les composantes covariantes d’un tenseur d’ordre deux.

2.

Le produit tensoriel des quantités $\delta _{i}^{j}$ par les composantes covariantes $v_{k}$ d’un tenseur d’ordre un, nous donne les qantités : $\delta ^{i}_{j}\,v_{k}\,\,\,;i,j,k=1\,\,\text {\`a}\,\,n$.

La contraction sur les indices $j$ et $k$ donne les $n$ quantités :

\begin{equation*} \delta_{i}^{j}\,v_{j}=v_{i}
\tag{3.8.21} \end{equation*}

Les quantités $v_{i}$ étant les composantes covariantes d’un tenseur d’ordre un, les quantités $\delta _{i}^{j}$ sont, selon le critère général de tensorialité, les composantes mixtes d’un tenseur d’ordre deux.

Exercice 3.4

Notons $h_{i}$ $i=1,2,3$, les quantités de chaleur qui traversent l’unité d’aire d’un matériau durant l’unité de temps, dans des directions respectivement normales aux axes $0x_{i}$. Cette chaleur s’écoule sous l’influence d’un gradient de température $T$. Les quatités $h_{i}$ forment les composantes d’un vecteur noté $\mathbf {h}$. Dans un matériau anisotrope, la conduction thermique obéit à la loi de Fourier :

\begin{equation} h_{i}=-k_{ij}\,\dfrac{\partial\,T}{\partial\,x_{j}}
\tag{3.8.22}
\label{3.8.22} \end{equation}

1.

Démontrer que les coefficients $k_{ij}$ sont les composantes d’un tenseur appelé tenseur de conductivité thermique.

2.

En régime permanent, l’écoulement de la chaleur à travers un matériau est conservatif, c’est-à-dire qu’on a :

\begin{equation} \text{div}\,\beq{h}=0
\tag{3.8.23}
\label{3.8.23} \end{equation}

Déterminer l’équation donnant la distribution des températures $T(x,y,z)$ à l’intérieur d’un matériau anisotrope. On supposera que les coefficients $k_{ij}$ sont des constantes.

3.

Déterminer l’expression de l’équation obtenue à la question (2) dans le système d’axes principaux du tenseur $k_{ij}$.

4.

Trouver un changement de variables qui permet de mettre l’équation obtenue à la question précédente sous forme d’une équation de Laplace :

\begin{equation} (k_{1}\,k_{2}\,k_{3})^{1/3}\,\Delta\,T=0
\tag{3.8.24}
\label{3.8.24} \end{equation}

où les $k_{i}$ sont les composantes non nulles du tenseur dans son système d’axes principaux.

Solutions

1.

Les composantes du vecteur $\mathbf {grad}$ $T$ qui figurent dans l’équation (3.8.22) forment un produit contracté avec les quantités $k_{ij}$ pour donner les composantes d’un vecteur. Selon le critère général de tensorialité, les coefficients $k_{ij}$ forment donc les composantes d’un tenseur d’ordre deux.

2.

Reportons l’expression de $h_{i}$ donné par (3.8.22) dans l’équation de conservation (3.8.23) qu’on peut écrire sous forme indicielle :

\begin{equation} \dfrac{\partial\,h_{i}}{\partial\,x_{i}}=0
\tag{3.8.25}
\label{3.8.25} \end{equation}

\begin{equation} \dfrac{\partial}{\partial\,x_{i}}\bigg(-k_{ij}\,\dfrac{\partial\,T}{\partial\,x_{j}}\bigg)=0
\tag{3.8.26}
\label{3.8.26} \end{equation}

C’est l’équation des distributions des température en régime stationnaire. En général, les $k_{ij}$ varient très faiblement dans un intervalle de température relativement important et on peut alors écrire l’équation (3.8.26) sous la forme :

\begin{equation} k_{ij}\,\dfrac{\partial^{2}\,T}{\partial\,x_{i}\,\partial\,x_{j}}=0
\tag{3.8.27}
\label{3.8.27} \end{equation}

3.

Dans un système d’axes principaux, le tenseur de conductivité thermique prend la forme : $k_{ij}=0$ si $i\,\neq \,j$, $k_{1}=k_{11}$, $k_{2}=k_{22}$, $k_{3}=k_{33}$. L’équation (3.8.27) se réduit alors à :

\begin{equation} k_{1}\,\dfrac{\partial^{2}\,T}{\partial\,x_{1}^{2}}+k_{2}\,\dfrac{\partial^{2}\,T}{\partial\,x_{2}^{2}}+k_{3}\,\dfrac{\partial^{2}\,T}{\partial\,x_{3}^{2}}=0
\tag{3.8.28}
\label{3.8.28} \end{equation}

4.

Le changement de variable suivant :

\begin{equation} x_{1}=\dfrac{k_{1}^{1/2}}{(k_{1}\,k_{2}\,k_{3})^{1/6}}\,X_{1}\,\,;\,\,x_{2}=\dfrac{k_{2}^{1/2}}{(k_{1}\,k_{2}\,k_{3})^{1/6}}\,X_{2}\,\,;\,\,x_{3}=\dfrac{k_{3}^{1/2}}{(k_{1}\,k_{2}\,k_{3})^{1/6}}\,X_{3}
\tag{3.8.29}
\label{3.8.29} \end{equation}

transforme l’équation (3.8.28) sous la forme :

\begin{equation} (k_{1}\,k_{2}\,k_{3})^{1/3}\,\bigg(\dfrac{\partial^{2}\,T}{\partial\,X_{1}^{2}}+\dfrac{\partial^{2}\,T}{\partial\,X_{2}^{2}}+\dfrac{\partial^{2}\,T}{\partial\,X_{3}^{2}}\bigg)=0
\tag{3.8.30}
\label{3.8.30} \end{equation}

On obtient une équation de Laplace correspondant à un écoulement dans un milieu isotrope de conductivité $(k_{1}\,k_{2}\,k_{3})^{1/3}$. On peut ainsi résoudre plus aisément l’équation (3.8.28) et obtenir ensuite la distribution des températures dans un milieu anisotrope.

Exercice 3.5

Soit $T_{ik}$ un tenseur du second ordre. On se propose de trouver tous les vecteurs $\mathbf {A}$, de composantes $A_{k}\,\,\,k=1,2,3$, qui ne changent pas d’orientation lorsqu’on effectue leur produit contracté avec le tenseur $T_{ik}$, c’est-à-dire tous les vecteurs tels que :

\begin{equation} T_{ik}\,A_{k}=\lambda\,A_{i}
\tag{3.8.31}
\label{3.8.31} \end{equation}

où $\lambda $ est un scalaire quelconque. De tels vecteurs, s’ils existent, sont appelés les vecteurs propres du tenseur et leurs directions sont les directions principales de $T_{ik}$. Les valeurs de $\lambda $ pour lesquelles l’équation (3.8.31) a des solutions s’appellent les valeurs propres du tenseur ; ce sont les valeurs des composantes $T_{ik}$ dans le système de coordonnées déterminé par les directions principales.

A titre d’exercice, nous allons déterminer les vecteurs et valeurs propres d’un tenseur $T_{ik}$ pour un système physique à deux dimensions. C’est le cas, par exemple, du tenseur d’inertie d’une ou plusieurs particules se mouvant dans un plan. Le tenseur possède ainsi quatre composantes :

\begin{equation} T_{11}\,T_{12}\,T_{21}\,T_{22}
\tag{3.8.32}
\label{3.8.32} \end{equation}

Supposons de plus que le tenseur soit symétrique : $T_{12}=T_{21}$, afin de simpifier les calculs.

1.

Écrire de manière développée les équations (3.8.31).

2.

Déterminer les valeurs propres du tenseur.

3.

Si $T_{12}=0$, les axes initiaux sont précisément les axes principaux. On suppose par la suite que $T_{12}\,\neq \,0$. Déterminer les pentes des axes principaux portant les vecteurs propres.

4.

Soient $\varphi _{1}$ et $\varphi _{2}$ les angles respectifs entre l’axe initial $Ox_{1}$ et les axes principaux du tenseur $T_{ik}$. Calculer tan $\varphi _{1}$ et tan $\varphi _{2}$ et montrer que les axes principaux sont orthogonaux entre eux.

5.

Quelles sont les valeurs des composantes des vecteurs $\mathbf {A}$ dans le système d’axes principaux du tenseur ?

6.

Déterminer les valeurs $T'_{ik}$ des composantes du tenseur dans son système d’axes principaux.

7.

Déterminer la courbe représentée par l’équation :

\begin{equation} T’_{11}\,(x’_{1})^{2}+T’_{22}\,(x’_{2})^{2}=1
\tag{3.8.33}
\label{3.8.33} \end{equation}

dans un système de coordonnées $x'_{1}$, $x'_{2}$, correspondant aux axes principaux.

8.

Démontrer que les grandeurs $C_{1}=T_{11}+T_{22}$ et $C_{2}=T_{11}\,T_{22}-T_{12}^{2}$ sont des invariants pour tout changement de système d’axes.

9.

Donner une interprétation géométrique de $C_{2}$.

Solutions

1.

Si le vecteur $\mathbf {A}$ est porté par l’un des axes principaux du tenseur $T_{ik}$, alors ses composantes $A_{j}$ doivent vérifier les équations suivantes :

\begin{equation*} T_{11}\,A_{1}+T_{12}\,A_{2}=\lambda\,A_{1}
\tag{3.8.34} \end{equation*}

\begin{equation} T_{21}\,A_{1}+T_{22}\,A_{2}=\lambda\,A_{2}
\tag{3.8.35}
\label{3.8.35} \end{equation}

2.

Le système d’équations (3.8.35) possède une solution différente de zéro si et seulement si le déterminant du système est nul, soit :

\begin{equation} \left| \begin{array}{cc}
         T_{11}-\lambda  & T_{12}  \\
  \\
T_{12}  & T_{22}-\lambda \\
     \end{array} \right | =0
\tag{3.8.36}
\label{3.8.36} \end{equation}

Le développement du déterminant conduit à l’équation :

\begin{equation} \lambda^{2}-\lambda\,(T_{11}-T_{22})+(T_{11}\,T_{22}-T_{12}^{2})=0
\tag{3.8.37}
\label{3.8.37} \end{equation}

dont les solutions sont les suivantes :

\begin{equation} \lambda\,\pm\,=\dfrac{T_{11}+T_{22}}{2}\,\pm\,\sqrt{\bigg(\dfrac{T_{11}-T_{22}}{2}\bigg)^{2}+T_{12}^{2}}
\tag{3.8.38}
\label{3.8.38} \end{equation}

Les valeurs $\lambda _{+}$ et $\lambda _{-}$ sont les valeurs propres du tenseur.

3.

Posons $\lambda _{+}=\lambda _{1}$ et $\lambda _{-}=\lambda _{2}$ ; Si $T_{12}\,\neq \,0$, alors $\lambda _{1}\,\neq \,\lambda _{2}$. On a donc deux axes principaux distincts déterminés par les vecteurs notés $\beq {A}^{(1)}$ et $\beq {A}^{(2)}$ et correspondent respectivement à $\lambda _{1}$ et $\lambda _{2}$. Les équations (3.8.35) permettent d’obtenir les pentes des axes principaux :

\begin{align} \tag{3.8.39}
\label{3.8.39}
\text{tan}\,\varphi_{1} &= \dfrac{A_{2}^{(1)}}{A_{1}^{(1)}} = \dfrac{\lambda_{1}-T_{11}}{T_{12}} = \dfrac{T_{12}}{\lambda_{1}-T_{22}} \\
\tag{3.8.40}
\label{3.8.40}
\text{tan}\,\varphi_{2} &= \dfrac{A_{2}^{(2)}}{A_{1}^{(2)}} = \dfrac{\lambda_{2}-T_{11}}{T_{12}} = \dfrac{T_{12}}{\lambda_{2}-T_{22}} \end{align}

Les angles $\varphi _{1}$ et $\varphi _{2}$ sont respectivement les angles entre l’axe $Ox_{1}$ et les axes principaux du tenseur $T_{ik}$.

4.

Substituant les valeurs $\lambda _{1}$ et $\lambda _{2}$ données par (3.8.38) dans les expressions (3.8.39) et (3.8.40), on obtient :

\begin{equation} \text{tan}\,2\,\varphi_{1}=\dfrac{2\,\text{tan}\,\varphi_{1}}{1-\text{tan}^{2}\,\varphi_{1}}=\dfrac{2\,T_{12}}{T_{11}-T_{22}}=\text{tan}\,2\,\varphi_{2}
\tag{3.8.41}
\label{3.8.41} \end{equation}

En conséquence :

\begin{equation} \varphi_{1}=\varphi_{2}+\dfrac{\pi}{2}
\tag{3.8.42}
\label{3.8.42} \end{equation}

Les axes principaux sont orthogonaux entre eux.

5.

Les vecteurs $\beq {A}^{(1)}$ et $\beq {A}^{(2)}$ étant portés par les axes principaux, leurs composantes, dans ce système d’axes, sont tels que :

\begin{equation} A’^{(1)}_{1}\,\neq\,0\,\,\,\,;\,\,\,\,A’^{(1)}_{2}=0\,\,\,\,;\,\,\,\,A’^{(2)}_{1}=0\,\,\,\,;\,\,\,\,A’^{(2)}_{2}\,\neq\,0
\tag{3.8.43}
\label{3.8.43} \end{equation}

6.

Les équations (3.8.35) s’écrivent, pour $\lambda =\lambda _{1}$, compte tenu de (3.8.41) :

\begin{equation} T’_{11}\,A’^{(1)}_{1}=\lambda_{1}\,A’^{(1)}_{1}\,\,\,\,;\,\,\,\,T’_{21}\,A’^{(1)}_{1}=\lambda_{1}\,A’^{(1)}_{2}=0
\tag{3.8.44}
\label{3.8.44} \end{equation}

d’où :

\begin{equation} T’_{11}=\lambda_{1}\,\,\,\,;\,\,\,\,T’_{21}=0
\tag{3.8.45}
\label{3.8.45} \end{equation}

Pour $\lambda =\lambda _{2}$, on obtient :

\begin{equation} T’_{12}\,A’^{(2)}_{2}=\lambda_{2}\,A’^{(2)}_{1}\,\,\,\,;\,\,\,\,T’_{22}\,A’^{(2)}_{2}=\lambda_{2}\,A’^{(2)}_{2}
\tag{3.8.46}
\label{3.8.46} \end{equation}

d’où :

\begin{equation} T’_{12}=0\,\,\,\,;\,\,\,\,T’_{22}=\lambda_{2}
\tag{3.8.47}
\label{3.8.47} \end{equation}

Dans son sytème d’axes principaux, le tenseur $T_{ik}$ a pour représentation matricielle :

\begin{equation*} [T’_{ik}]=\begin{bmatrix}
T’_{11}&0 \\
0&T’_{22}
\end{bmatrix}=\begin{bmatrix}
\lambda_{1}&0 \\
0&\lambda_{2}
\end{bmatrix}
\tag{3.8.48}
\label{3.8.48} \end{equation*}

7.

Dans le système d’axes principaux, les valeurs des composantes du tenseur permettent d’écrire l’équation (3.8.33) sous la forme :

\begin{equation} \lambda_{1}\,(x’_{1})^{2}+\lambda_{2}\,(x’_{2})^{2}=1
\tag{3.8.49}
\label{3.8.49} \end{equation}

soit encore :

\begin{equation} \dfrac{(x’_{1})^{2}}{1/\lambda_{1}}+\dfrac{(x’_{2})^{2}}{1/\lambda_{2}}=1
\tag{3.8.50}
\label{3.8.50} \end{equation}

C’est l’équation d’une ellipse dont les demi-axes ont pour longueur $1/\sqrt {\lambda _{1}}$ et $1/\sqrt {\lambda _{2}}$. C’est l’ellipse représentative du tenseur $T_{ik}$.

8.

Les nombres $\lambda $ et $\lambda ^{2}$ qui figurent dans l’équation(3.8.37) sont des scalaires ; les racines $\lambda _{1}$et $\lambda _{2}$ de l’équation donnent les valeurs $1/\lambda _{1}$ et $1/\lambda _{2}$ qui sont les longueurs des demi-axes de l’ellipse du tenseur. Par suite, ces nombres sont indépendants du système d’axes choisi et il en est de même de leurs coefficients dans l’équation (3.8.37). Les quantités :

\begin{equation} C_{1}=T_{11}+T_{22}\,\,\,\,;\,\,\,\,C_{2}=T_{11}\,T_{22}-T_{12}^{2}
\tag{3.8.51}
\label{3.8.51} \end{equation}

sont donc des invariants du tenseur $T_{ik}$.

9.

Dans le système d’axes principaux, la valeur de $C_{2}$ est égale à $C_{2}=\lambda _{1}\,\lambda _{2}$. D’autre part, la surface $S$ d’une ellipse de demi-axes $a$ et $b$, est donnée par :

\begin{equation} S=\pi\,a\,b
\tag{3.8.52}
\label{3.8.52} \end{equation}

Dans le cas présent, on a : $a=1/\sqrt {\lambda _{1}}$, $b=1/\sqrt {\lambda _{2}}$, d’où :

\begin{equation} S=\pi\,\sqrt{\dfrac{1}{\lambda_{1}\,\lambda_{2}}}=\pi\,\sqrt{\dfrac{1}{C_{2}}}
\tag{3.8.53}
\label{3.8.53} \end{equation}

Ainsi l’invariance de $C_{2}$ exprime le fait que la surface de l’ellipse représentative du tenseur est constante dans tous les systèmes de coordonnées.

Remarque : Dans le cas d’un tenseur d’ordre deux d’un espace à trois dimensions, on obtient un ellipsoïde de représentation du tenseur (voir exercice 2.6).

Exercice 3.6

La construction suivante, due à Otto Mohr (1835-1918), est utile pour l’étude des tenseurs symétriques de rang deux. Elle est employée, par exemple, par les ingénieurs dans l’analyse des déformations et des contraintes.

1.

Soit un système d’axes $Ox_{1}$,$Ox_{2}$,$Ox_{3}$. Une rotation du système d’un angle $\alpha $ autour de l’axe $Ox_{3}$ donne les nouveaux axes $Ox'_{1}$,$Ox'_{2}$,$Ox'_{3}$. Déterminer la matrice de passage des $x_{i}$ aux $x'_{j}$.

2.

Considérons un tenseur $S_{ij}$ ayant pour axes principaux $Ox_{1}$,$Ox_{2}$,$Ox_{3}$. Dans ce système d’axes, le tenseur a pour seules composantes non nulles $S_{1}=S_{11}$, $S_{2}=S_{22}$, $S_{3}=S_{33}$. Déterminer les expressions des composantes $S'_{ij}$ de ce tenseur dans le système d’axes $Ox'_{1}$,$Ox'_{2}$,$Ox'_{3}$ en fonction des composantes $S_{k}$.

3.

Écrire les expressions des $S'_{ij}$ en fonction de l’angle $2\,\alpha $. On rappelle les relations suivantes :

\begin{equation} \text{cos}\,2\,\alpha=2\,\text{cos}^{2}\,\alpha-1=1-2\,\text{sin}^{2}\,\alpha\,\,\,\,;\,\,\,\,\text{sin}\,2\,\alpha=2\,\text{sin}\,\alpha\,\text{cos}\,\alpha
\tag{3.8.54}
\label{3.8.54} \end{equation}

4.

On suppose que $S_{1}

5.

Réciproquement, si on se donne les valeurs $S'_{ij}$, montrer que le cercle de Mohr permet de trouver les composantes principales $S_{ij}$ du tenseur ainsi que la direction des axes principaux.

6.

La construction du cercle de Mohr reste valable si l’axe de rotation $Ox_{3}$ n’est plus un axe principal du tenseur. Si on considère une section centrale arbitraire de l’ellipsoïde représentative du tenseur, on obtient une conique ; soit alors $Ox_{1}$ et $Ox_{2}$ les axes principaux de cette section. Par rapport aux axes $Ox_{1}$, $Ox_{2}$ et $Ox_{3}$ normal à la section considérée, le tenseur prend la forme :

\begin{equation} \begin{bmatrix}
S_{11}&0&S_{31} \\
0&S_{22}&S_{23} \\
S_{31}&S_{23}&S_{33}
\end{bmatrix}
\tag{3.8.55}
\label{3.8.55} \end{equation}

Déterminer les composantes $S'_{ij}$ du tenseur après une rotation d’un angle $\alpha $ autour de l’axe $Ox_{3}$. Montrer que la construction du cercle de Mohr s’applique également dans ce cas.

Solutions

1.

Ce calcul a déjà été realisé au cours de l’exercice 1.10. On obtient :

\begin{equation} \begin{bmatrix}
\text{cos}\,\alpha&\text{sin}\,\alpha&0 \\
-\text{sin}\,\alpha&\text{cos}\,\alpha&0 \\
0&0&1
\end{bmatrix}
\tag{3.8.56}
\label{3.8.56} \end{equation}

2.

Le changement de référentiel donne pour expression des composantes $S'_{kl}$ dans le référentiel $Ox'_{1}$, $Ox'_{2}$, $Ox'_{3}$, selon la formule (2.1.12) :

\begin{equation} S’_{kl}=A’^{k}_{i}\,A’^{l}_{j}\,S_{ij}
\tag{3.8.57}
\label{3.8.57} \end{equation}

Les référentiels étant orthogonaux, les composantes contravariantes et covariantes sont identiques. La matrice de passage (3.8.56) donne pour expression des nouvelles composantes :

\begin{align}   S’_{11} &= A’^{1}_{1}\,A’^{1}_{1}\,S_{11}+A’^{1}_{2}\,A’^{1}_{2}\,S_{22} = S_{1}\,\text{cos}^{2}\,\alpha+S_{2}\,\text{sin}^{2}\,\alpha\\
  S’_{22} &= S_{1}\,\text{sin}^{2}\,\alpha+S_{2}\,\text{cos}^{2}\,\alpha\\
  S’_{12} &= S’_{21} = (-S_{1}+S_{2})\,\text{sin}\,\alpha\,\text{cos}\,\alpha\\
  S’_{33} &= S_{3}
\tag{3.8.58}
\label{3.8.58} \end{align}

Les autres composantes $S'_{ij}$ du tenseur sont nulles. Le tenseur transformé a donc pour matrice :

\begin{equation} \begin{bmatrix}
S’_{11}&S’_{12}&0 \\
S’_{12}&S’_{22}&0 \\
0&0&S_{3}
\end{bmatrix}
\tag{3.8.59}
\label{3.8.59} \end{equation}

3.

Compte tenu des relations (3.8.54), les expressions (3.8.56) s’écrivent sous la forme :

\begin{equation*} S’_{11}=\dfrac{1}{2}(S_{1}+S_{2})-(S_{2}-S_{1})\,\text{cos}\,2\,\alpha
\tag{3.8.60} \end{equation*}

\begin{equation*} S’_{22}=\dfrac{1}{2}(S_{1}+S_{2})+(S_{2}-S_{1})\,\text{cos}\,2\,\alpha
\tag{3.8.61} \end{equation*}

\begin{equation} S’_{12}=\dfrac{1}{2}(S_{2}-S_{1})\,\text{sin}\,2\,\alpha
\tag{3.8.62}
\label{3.8.62} \end{equation}

4.

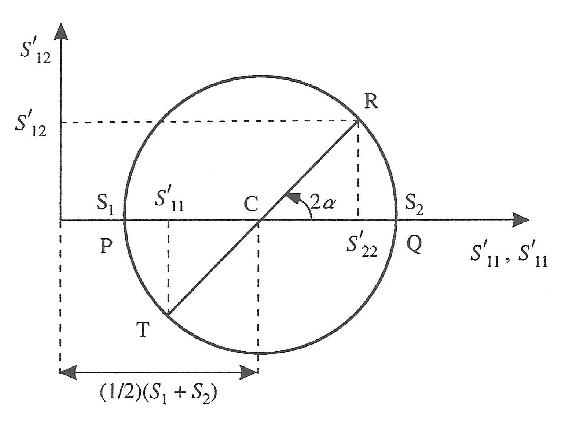
La figure 3.1 montre le cercle de centre $C$ centré sur l’axe des abscisses.

figure 3.1:

On trace le diamètre $TCR$, tel que $CR$ fasse avec $CQ$ un angle $2\,\alpha $ mesuré dans le sens inverse des aiguilles d’une montre. Puisque $OC=(1/2)(S_{1}+S_{2})$ et que $CR=(1/2)(S_{2}-S_{1})$, les équations (3.8.62) montrent que les coordonnées du point $R$, par rapport aux axes du graphique, sont égaux à $S'_{22}$ et $S'_{12}$. D’autre part, le point $T$ a pour abscisse $S'_{11}$. Le cercle de Mohr montre ainsi comment les composantes $S'_{11}$, $S'_{22}$ et $S'_{12}$ varient lors d’une rotation des axes de référence.

La construction du cercle de Mohr reste évidemment valable lorsque $S_{1}$ et $S_{2}$ sont négatifs ou s’ils sont de signes opposés.

5.

Si l’on se donne les valeurs $S'_{11}$, $S'_{22}$ et $S'_{12}$, on peut déterminer les points $R$ et $T$ sur un graphique, leurs coordonnées étant :

\begin{equation} R=(S’_{22},S’_{12})\,\,\,\,;\,\,\,\,T=(S’_{11},-S’_{12})
\tag{3.8.64}
\label{3.8.64} \end{equation}

Les points $R$ et $T$ permettent de déterminer le centre du cercle et son diamètre. Le tracé du cercle donne les points d’intersection $P$ et $Q$ avec l’axe des abscisses, ces points donnant les valeurs $S_{1}$ et $S_{2}$ des composantes principales du tenseur. D’autre part, l’angle $\alpha $ est donné par :

\begin{equation} \text{tan}\,2\,\alpha=\dfrac{2\,S’_{12}}{S’_{22}-S’_{11}}
\tag{3.8.65}
\label{3.8.65} \end{equation}

6.

La matrice de rotation (3.8.56) subsiste mais les axes $Ox_{i}$ considérés à présent ne sont plus les axes principaux. Le changement de référentiel par rotation transforme les composantes selon la formule générale (3.8.57). On obtient :

\begin{equation*} S’_{11}=S_{11}\,\text{cos}^{2}\,\alpha+S_{22}\,\text{sin}^{2}\,\alpha\,\,\,\,;\,\,\,\,S’_{22}=S_{11}\,\text{sin}^{2}\,\alpha+S_{22}\,\text{cos}^{2}\,\alpha
\tag{3.8.66} \end{equation*}

\begin{equation*} S’_{12}=S’_{21}=(-S_{11}+S_{22})\,\text{sin}\,\alpha\,\text{cos}\,\alpha\,\,\,\,;\,\,\,\,S’_{33}=S_{33}
\tag{3.8.67} \end{equation*}

\begin{equation} S’_{23}=-S_{13}\,\text{sin}\,\alpha+S_{23}\,\text{cos}\,\alpha\,\,\,\,;\,\,\,\,S’_{31}=S_{13}\,\text{cos}\,\alpha+S_{23}\,\text{sin}\,\alpha
\tag{3.8.68}
\label{3.8.68} \end{equation}

En ce qui concerne tout au moins $S'_{11}$, $S'_{22}$, $S'_{12}$, on obtient les mêmes formules qu’en (3.8.58) et la construction du cercle de Mohr s’applique également.

Exercice 3.7

Soient deux opérateurs linéaires $A$ et $B$ agissant respectivement sur les vecteurs des espaces vectoriels $\varepsilon _{p}$ et $\varepsilon _{q}$. On note $\Psi $ les vecteurs de $\varepsilon _{p}$ et $\Phi $ ceux de $\varepsilon _{q}$ ; l’espace produit tensoriel de $\varepsilon _{p}$ et $\varepsilon _{q}$ est noté $\varepsilon _{pq}$=$\varepsilon _{p}$$\,\otimes \,$$\varepsilon _{q}$. Par définition, l’opérateur noté :

\begin{equation} A\,\otimes\,B=C
\tag{3.8.69}
\label{3.8.69} \end{equation}

est l’opérateur qui, agissant sur un vecteur $\Psi \,\otimes \,\Phi $ de l’espace $\varepsilon _{pq}$, donne le vecteur :

\begin{equation} C\,(\Psi\,\otimes\,\Phi)=(A\,\otimes\,B)\,(\Psi\,\otimes\,\Phi)=A\,\Psi\,\otimes\,B\,\Phi
\tag{3.8.70}
\label{3.8.70} \end{equation}

L’opérateur $A\,\otimes \,B$ est appelé le produit tensoriel des opérateurs $A$ et $B$.

1.

Soient les produits d’opérateurs $A_{1}\,A_{2}$ et $B_{1}\,B_{2}$ agissant respectivement dans les espaces $\varepsilon _{p}$et $\varepsilon _{q}$. Montrer qu’on a :

\begin{equation} A_{1}\,A_{2}\,\otimes\,B_{1}\,B_{2}=(A_{1}\,\otimes\,B_{1})\,(A_{2}\,\otimes\,B_{2})
\tag{3.8.71}
\label{3.8.71} \end{equation}

2.

Montrer que l’opérateur $A^{-1}\,\otimes \,B^{-1}$ est l’opérateur inverse de $A\,\otimes \,B$.

3.

On note $\Psi $ un vecteur propre d’un opérateur $A$ agissant dans $\varepsilon _{p}$, c’est-à-dire un vecteur tel que :

\begin{equation} A\,\Psi=\alpha\,\Psi
\tag{3.8.72}
\label{3.8.72} \end{equation}

où $\alpha $ est un nombre appelé valeur propre associée à $\Psi $. De même, on considère un vecteur $\Phi $ qui est vecteur propre de l’opérateur $B$ agissant dans $\varepsilon _{q}$, associè à la valeur propre $\beta $. Montrer que les vecteurs $\Psi \,\otimes \,\Phi $ sont des vecteurs propres des opérateurs $A\,\otimes \,\dsone _{q}$ et $\dsone _{p}\,\otimes \,B$, où $\dsone _{q}$ et $\dsone _{p}$ sont des opérateurs unité agissant respectivement dans $\varepsilon _{p}$ et $\varepsilon _{q}$. Déterminer les valeurs propres respectives de ces opérateurs.

4.

Déterminer les vecteurs propres et valeurs propres des opérateurs $(A\,\otimes \,\dsone _{q})^{2}$ et $(\dsone _{p}\,\otimes \,B)^{2}$.

5.

Soient {$\Psi _{i}$} et {$\Phi _{j}$} des bases respectives de $\varepsilon _{p}$ et $\varepsilon _{q}$. Les éléments matriciels respectifs $a_{ki}$ et $b_{lj}$ des opérateurs $A$ et $B$ sont définis par :

\begin{equation} A\,\Psi_{i}=\sum_{k}\,a_{ki}\,\Psi_{k}\,\,\,\,;\,\,\,\,B\,\Phi_{j}=\sum_{l}\,b_{lj}\,\Phi_{l}
\tag{3.8.73}
\label{3.8.73} \end{equation}

Déterminer les éléments matriciels de l’opérateur $A\,\otimes \,B$.

Solutions

1.

La définition (3.8.70) nous donne :

\begin{equation} (A_{1}\,A_{2}\,\otimes\,B_{1}\,B_{2})=[A_{1}\,(A_{2}\,\Psi)]\,\otimes\,[B_{1}\,(B_{2}\,\Phi)]
\tag{3.8.74}
\label{3.8.74} \end{equation}

Utilisant la définition (3.8.70) en sens inverse, on obtient :

\begin{equation} [A_{1}\,(A_{2}\,\Psi)]\,\otimes\,[B_{1}\,(B_{2}\,\Phi)]=(A_{1}\,\otimes\,B_{1})\,(A_{2}\,\Psi\,\otimes\,B_{2}\,\Phi)
\tag{3.8.75} \end{equation}

\begin{equation} =(A_{1}\,\otimes\,B_{1})\,(A_{2}\,\otimes\,B_{2})\,(\Psi\,\otimes\,\Phi)
\tag{3.8.76}
\label{3.8.76} \end{equation}

Les vecteurs $\Psi $ et $\Phi $ étant quelconques, les relations (3.8.74) et (3.8.76) donnent :

\begin{equation} (A_{1}\,A_{2}\,\otimes\,B_{1}\,B_{2})=(A_{1}\,\otimes\,B_{1})\,(A_{2}\,\otimes\,B_{2})
\tag{3.8.77}
\label{3.8.77} \end{equation}

2.

La relation (3.8.77) permet d’écrire :

\begin{equation} (A\,\otimes\,B)\,(A^{-1}\,\otimes\,B^{-1})=(A\,A^{-1})\,\otimes\,(B\,B^{-1})=\dsone_{p}\,\otimes\,\dsone_{q}
\tag{3.8.78}
\label{3.8.78} \end{equation}

Selon la définition (3.8.70), on obtient :

\begin{equation} (\dsone_{p}\,\otimes\,\dsone_{q})\,(\Psi\,\otimes\,\Phi)=\dsone_{p}\,\Psi\,\otimes\,\dsone_{q}\,\Phi=\Psi\,\otimes\,\Phi
\tag{3.8.79}
\label{3.8.79} \end{equation}

L’opérateur $\dsone _{p}\,\otimes \,\dsone _{q}$ est donc l’opérateur unité agissant dans $\varepsilon _{p}$$\,\otimes \,$$\varepsilon _{q}$, d’où :

\begin{equation} (A\,\otimes\,B)\,(A^{-1}\,\otimes\,B^{-1})=\dsone_{pq}
\tag{3.8.80}
\label{3.8.80} \end{equation}

En conséquence, l’opérateur $(A^{-1}\,\otimes \,B^{-1})$ est l’opérateur inverse de $A\,\otimes \,B$ :

\begin{equation} (A\,\otimes\,B)^{-1}=A^{-1}\,\otimes\,B^{-1}
\tag{3.8.81}
\label{3.8.81} \end{equation}

3.

La définition (3.8.70) du produit tensoriel de deux opérateurs ainsi que la relation (3.8.72), nous donnent :

\begin{equation} (A\,\otimes\,\dsone_{q})\,(\Psi\,\otimes\,\Phi)=A\,\Psi\,\otimes\,\dsone_{q}\,\Phi=(\alpha\,\Psi)\,\otimes\,\Phi=\alpha\,(\Psi\,\otimes\,\Phi)
\tag{3.8.82}
\label{3.8.82} \end{equation}

Les vecteurs $\Psi \,\otimes \,\Phi $ de $\varepsilon _{p}$$\,\otimes \,$$\varepsilon _{q}$ sont des vecteurs de $(A\,\otimes \,\dsone _{q})$ associés à la valeur propre $\alpha $. Une démonstration analogue montre que les vecteurs $\Psi \,\otimes \,\Phi $ sont des vecteurs propres de $\dsone _{p}\,\otimes \,B$ associés à la valeur propre $\beta $.

4.

L’application de l’opérateur $(A\,\otimes \,\dsone _{q})^{2}$ aux vecteurs $\Psi \,\otimes \,\Phi $ donne, selon (3.8.82) :

\begin{equation} (A\,\otimes\,\dsone_{q})^{2}\,(\Psi\,\otimes\,\Phi)=(A\,\otimes\,\dsone_{q})\,\alpha(\Phi\,\otimes\,\Psi)=\alpha^{2}\,(\Psi\,\otimes\,\Phi)
\tag{3.8.83}
\label{3.8.83} \end{equation}

Les vecteurs $\Psi \,\otimes \,\Phi $ sont des vecteurs propres de l’opérateur $(A\,\otimes \,\dsone _{q})^{2}$ associés à la valeur propre $\alpha ^{2}$. On montre de même que les vecteurs $\Psi \,\otimes \,\Phi $ sont également des vecteurs propres de l’opérateur $(\dsone _{p}\,\otimes \,B)^{2}$ associés à la valeur propre $\beta ^{2}$.

5.

Utilisant la propriété de distributivité (3.1.16) du produit tensoriel ainsi que l’associativité (3.1.17) par rapport à la multiplication par un scalaire, on obtient :

\begin{equation*} A\,\otimes\,B\,(\Psi_{i}\,\otimes\,\Phi_{j})=(A\,\Psi_{i})\,\otimes\,(B\,\Phi_{j})
\tag{3.8.84} \end{equation*}

\begin{equation*} =\bigg(\sum_{k}\,a_{ki}\,\Psi_{k}\bigg)\,\otimes\,\bigg(\sum_{l}\,a_{lj}\,\Psi_{l}\bigg)
\tag{3.8.85} \end{equation*}

\begin{equation} =\sum_{kl}\,(a_{ki}\,b_{lj})\,(\Psi_{k}\,\otimes\,\Phi_{l})
\tag{3.8.86}
\label{3.8.86} \end{equation}

[prev] [prev-tail] [front] [up]