Écrire les expressions suivantes en utilisant la convention de sommation ainsi que l’écriture indicielle (4.1.21) des dérivées partielles :
\begin{equation*}
\text{d}\Phi=\dfrac{\partial\,\Phi}{\partial\,x^{1}}\,\text{d}x^{1}+\dfrac{\partial\,\Phi}{\partial\,x^{2}}\,\text{d}x^{2}+...+\dfrac{\partial\,\Phi}{\partial\,x^{n}}\,\text{d}x^{n}
\tag{4.4.1}
\end{equation*}
\begin{equation*}
\dfrac{\text{d}f}{\text{d}t}=\dfrac{\partial\,\Phi}{\partial\,x^{1}}\,\dfrac{\text{d}x^{1}}{\text{d}t}+\dfrac{\partial\,\Phi}{\partial\,x^{2}}\,\dfrac{\text{d}x^{2}}{\text{d}t}+...+\dfrac{\partial\,\Phi}{\partial\,x^{n}}\,\dfrac{\text{d}x^{n}}{\text{d}t}
\tag{4.4.2}
\end{equation*}
\begin{equation*}
\text{d}s^{2}=g_{11}\,(\text{d}x^{1})^{2}+g_{12}\,\text{d}x^{1}\,\text{d}x^{2}+g_{21}\,\text{d}x^{2}\,\text{d}x^{1}+g_{22}\,(\text{d}x^{2})^{2}
\tag{4.4.3}
\end{equation*}
\begin{equation*}
\text{d}\Phi=\partial_{k}\,\Phi\,\text{d}x^{k}\,\,\,\,;\,\,\,\,k=1,...,n
\tag{4.4.4}
\end{equation*}
\begin{equation*}
\dfrac{\text{d}f}{\text{d}t}=\partial_{k}\,f\,\dfrac{\text{d}x^{k}}{\text{d}t};\,\,\,\,k=1,...,n
\tag{4.4.5}
\end{equation*}
\begin{equation*}
\text{d}s^{2}=g_{ij}\,\text{d}x^{i}\,\text{d}x^{j}\,\,\,\,;\,\,\,\,i,j=1,2
\tag{4.4.6}
\end{equation*}
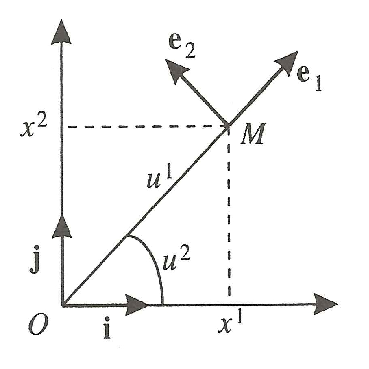
Les coordonnées polaires dans un plan $E_{2}$, représentés sur la figure 4.1, sont donnés par : $x^{1}=u^{1}\,\text {cos}\,u^{2}$ ; $x^{2}=u^{1}\,\text {sin}\,u^{2}$ ; où $x^{1}$ et $x^{2}$ sont les coordonnées cartésiennes, $u^{1}$ est la longueur $OM$ et $u^{2}$ l’angle des droites $OM$, $Ox^{1}$.
\begin{align*}
\beq{e_{1}} &= \dfrac{\partial\,\beq{M}}{\partial\,u^{1}} = \dfrac{\partial\,x^{1}}{\partial\,u^{1}}\,\beq{i}+\dfrac{\partial\,x^{2}}{\partial\,u^{1}}\,\beq{j} = (\text{cos}\,u^{2})\,\beq{i}+(\text{sin}\,u^{2})\,\beq{j}\\
\beq{e_{2}} &= \dfrac{\partial\,\beq{M}}{\partial\,u^{2}} = \dfrac{\partial\,x^{1}}{\partial\,u^{2}}\,\beq{i}+\dfrac{\partial\,x^{2}}{\partial\,u^{2}}\,\beq{j} = -(\,u^{1}\,\text{sin}\,u^{2})\,\beq{i}+(u^{1}\,\text{cos}\,u^{2})\,\beq{j}\\
\tag{4.4.8}
\end{align*}
\begin{equation*}
g_{11}=(\text{cos}\,u^{2})^{2}+(\text{sin}\,u^{2})^{2}=1\,\,\,;\,\,\,g_{12}=g_{21}=0\,\,\,;\,\,\,g_{22}=(u^{1})^{2}
\tag{4.4.9}
\end{equation*}
\begin{equation*}
\text{d}s^{2}=g_{ij}\,\text{d}u^{i}\,\text{d}u^{j}=(\text{d}u^{1})^{2}+(u^{1})^{2}\,(\text{d}u^{2})^{2}
\tag{4.4.10}
\end{equation*}
Un point $M$ est repéré en coordonnées cylindriques par les variables $\rho $,$\varphi $,$z$ (Fig.4.2).
\begin{equation*}
\beq{OM}(\rho,\varphi,z)=\rho\,\text{cos}\,\varphi\,\beq{i}+\rho\,\text{sin}\,\varphi\,\beq{j}+z\,\beq{k}
\tag{4.4.12}
\end{equation*}
\begin{align*}
\beq{e_{1}} &= \dfrac{\partial\,\beq{M}}{\partial\,\rho} = \text{cos}\,\varphi\,\beq{i}+\text{sin}\,\varphi\,\beq{j}\\
\beq{e_{2}} &= \dfrac{\partial\,\beq{M}}{\partial\,\varphi} = -\rho\,\text{sin}\,\varphi\,\beq{i}+\rho\,\text{cos}\,\varphi\,\beq{j}\\
\beq{e_{3}} &= \dfrac{\partial\,\beq{M}}{\partial\,z} = \beq{k}
\tag{4.4.13}
\end{align*}
\begin{align*}
\beq{e_{1}}\,\cdot\,\beq{e_{2}} &= (\text{cos}\,\varphi\,\beq{i}+\text{sin}\,\varphi\,\beq{j})\,\cdot\,(-\rho\,\text{sin}\,\varphi\,\beq{i}+\rho\,\text{cos}\,\varphi\,\beq{j}) = 0\\
\beq{e_{1}}\,\cdot\,\beq{e_{3}} &= (\text{cos}\,\varphi\,\beq{i}+\text{sin}\,\varphi\,\beq{j})\,\cdot\,\beq{k} = 0\\
\beq{e_{2}}\,\cdot\,\beq{e_{3}} &= (-\rho\,\text{sin}\,\varphi\,\beq{i}+\rho\,\text{cos}\,\varphi\,\beq{j})\,\cdot\,\beq{k} = 0
\tag{4.4.14}
\end{align*}
Les vecteurs $\mathbf {e_{1}}$, $\mathbf {e_{2}}$, $\mathbf {e_{3}}$ sont orthogonaux entre eux.
\begin{align*}
||\beq{e_{1}}|| = \sqrt{g_{11}} &= \sqrt{(\text{cos}\,\varphi\,\beq{i}+\text{sin}\,\varphi\,\beq{j})^{2}} = \sqrt{\text{cos}^{2}\,\varphi+\text{sin}^{2}\,\varphi} = 1\\
||\beq{e_{2}}|| = \sqrt{g_{22}} &= \sqrt{(-\rho\,\text{sin}\,\varphi\,\beq{i}+\rho\,\text{cos}\,\varphi\,\beq{j})^{2}} = \rho\\
||\beq{e_{3}}|| = \sqrt{g_{33}} &= \sqrt{\beq{k}\,\cdot\,\beq{k}} = 1
\tag{4.4.15}
\end{align*}
On considère un système de coordonnées paraboloïdales d’un espace ponctuel $E_{3}$ : $x=u\,v\,\text {cos}\,\varphi $ ; $y=u\,v\,\text {sin}\,\varphi $ ; $z=(1/2)\,(v^{2}-u^{2})$, où $x$, $y$, $z$ sont les coordonnées cartésiennes. Les coordonnées curvilignes sont notées dans l’ordre : $u^{1}=u$, $u^{2}=v$, $u^{3}=\varphi $.
\begin{equation}
\beq{OM}(u,v,\varphi)=u\,v\,\text{cos}\,\varphi\,\beq{i}+u\,v\,\text{sin}\,\varphi\,\beq{j}+(1/2)\,(v^{2}-u^{2})\,\beq{k}
\tag{4.4.16}
\end{equation}
\begin{align*}
\beq{e_{1}} &= \dfrac{\partial\,\beq{M}}{\partial\,u} = v\,\text{cos}\,\varphi\,\beq{i}+v\,\text{sin}\,\varphi\,\beq{j}-u\,\beq{k}\\
\beq{e_{2}} &= \dfrac{\partial\,\beq{M}}{\partial\,v} = u\,\text{cos}\,\varphi\,\beq{i}+u\,\text{sin}\,\varphi\,\beq{j}+v\,\beq{k}\\
\beq{e_{3}} &= \dfrac{\partial\,\beq{M}}{\partial\,\varphi} = -u\,v\,\text{sin}\,\varphi\,\beq{i}+u\,v\,\text{cos}\,\varphi\,\beq{j}
\tag{4.4.17}
\end{align*}
\begin{align*}
\beq{e_{1}}\,\cdot\,\beq{e_{2}} &= u\,v\,\text{cos}^{2}\,\varphi+u\,v\,\text{sin}^{2}\,\varphi-u\,v = 0\\
\beq{e_{1}}\,\cdot\,\beq{e_{3}} &= 0\\
\beq{e_{2}}\,\cdot\,\beq{e_{3}} &= 0
\tag{4.4.18}
\end{align*}
Les vecteurs de la base naturelle sont orthogonaux entre eux.
\begin{align*}
||\beq{e_{1}}|| &= \sqrt{g_{11}}=\sqrt{v^{2}\,\text{cos}^{2}\,\varphi+v^{2}\,\text{sin}^{2}\,\varphi+u^{2}}=\sqrt{v^{2}+u^{2}}\\
||\beq{e_{2}}|| &= \sqrt{g_{22}}=\sqrt{u^{2}\,\text{cos}^{2}\,\varphi+u^{2}\,\text{sin}^{2}\,\varphi+v^{2}}=\sqrt{u^{2}+v^{2}}\\
||\beq{e_{3}}|| &= \sqrt{g_{33}}=\sqrt{u^{2}\,v^{2}\,\text{sin}^{2}\,\varphi+u^{2}\,v^{2}\,\text{cos}^{2}\,\varphi}=u\,v
\tag{4.4.19}
\end{align*}
\begin{equation*}
\text{d}s^{2}=(v^{2}+u^{2})\,(\text{d}u)^{2}+(u^{2}+v^{2})\,(\text{d}v)^{2}+u^{2}\,v^{2}\,(\text{d}\varphi)^{2}
\tag{4.4.20}
\end{equation*}
On considère un système de coordonnées curvilignes $u$, $v$, $w$ d’un espace ponctuel $E_{3}$. Démontrer que les vecteurs de la base naturelle {$\mathbf {e_{u}}$,$\mathbf {e_{v}}$,$\mathbf {e_{w}}$} constituent un système réciproque des vecteurs {$\nabla \,u$,$\nabla \,v$,$\nabla \,w$}.
Les coordonnées curvilignes sont données par la transformation :
\begin{equation*}
x=x(u,v,w)\,\,\,\,;\,\,\,\,y=y(u,v,w)\,\,\,\,;\,\,\,\,z=z(u,v,w)
\tag{4.4.21}
\end{equation*}
où $x,y,z$ sont les coordonnées cartésiennes de $E_{3}$. La transformation inverse est telle que :
\begin{equation*}
u=u(x,y,z)\,\,\,\,;\,\,\,\,v=v(x,y,z)\,\,\,\,;\,\,\,\,w=w(x,y,z)
\tag{4.4.22}
\end{equation*}
Écrivons les expressions de $\mathbf {e_{u}}$ et $\nabla \,u$ sur une base cartésienne {$\mathbf {i}$,$\mathbf {j}$,$\mathbf {k}$} :
\begin{equation*}
\beq{e_{u}}=\dfrac{\partial\,\beq{M}}{\partial\,u}=\dfrac{\partial\,x}{\partial\,u}\,\beq{i}+\dfrac{\partial\,y}{\partial\,u}\,\beq{j}+\dfrac{\partial\,z}{\partial\,u}\,\beq{k}\\
\tag{4.4.23}
\end{equation*}
\begin{equation*}
\nabla\,u=\dfrac{\partial\,u}{\partial\,x}\,\beq{i}+\dfrac{\partial\,u}{\partial\,y}\,\beq{j}+\dfrac{\partial\,u}{\partial\,z}\,\beq{k}\\
\tag{4.4.24}
\end{equation*}
Le produit scalaire de ces deux vecteurs s’écrit :
\begin{equation*}
\beq{e_{u}}\,\cdot\,\nabla\,u=\dfrac{\partial\,x}{\partial\,u}\,\dfrac{\partial\,u}{\partial\,x}+\dfrac{\partial\,y}{\partial\,u}\,\dfrac{\partial\,u}{\partial\,y}+\dfrac{\partial\,z}{\partial\,u}\,\dfrac{\partial\,u}{\partial\,z}\\
\tag{4.4.25}
\end{equation*}
La fonction $u(x,y,z)$ peut s’écrire sous la forme suivante :
\begin{equation*}
\dfrac{\text{d}u}{\text{d}u}=1=\dfrac{\partial\,u}{\partial\,x}\,\dfrac{\partial\,x}{\partial\,u}+\dfrac{\partial\,u}{\partial\,y}\,\dfrac{\partial\,y}{\partial\,u}+\dfrac{\partial\,u}{\partial\,z}\,\dfrac{\partial\,z}{\partial\,u}\\
\tag{4.4.26}
\end{equation*}
d’où : $\beq {e_{u}}\,\cdot \,\nabla \,u=1$. On obtient de même : $\beq {e_{v}}\,\cdot \,\nabla \,v=1$ ; $\beq {e_{w}}\,\cdot \,\nabla \,w=1$
Écrivons à présent la dérivée de $u(x,y,z)$ considérée comme fonction composée, par rapport à
$v$, il vient :
\begin{equation*}
\dfrac{\text{d}u}{\text{d}v}=0=\dfrac{\partial\,u}{\partial\,x}\,\dfrac{\partial\,x}{\partial\,v}+\dfrac{\partial\,u}{\partial\,y}\,\dfrac{\partial\,y}{\partial\,v}+\dfrac{\partial\,u}{\partial\,z}\,\dfrac{\partial\,z}{\partial\,v}\\
\tag{4.4.27}
\end{equation*}
d’où : $\beq {e_{v}}\,\cdot \,\nabla \,u=0$. On obtient de même :
$\beq {e_{u}}\,\cdot \,\nabla \,v=\beq {e_{u}}\,\cdot \,\nabla \,w=\beq {e_{v}}\,\cdot \,\nabla \,w=\beq {e_{v}}\,\cdot \,\nabla \,u=\beq {e_{w}}\,\cdot \,\nabla \,u=\beq {e_{w}}\,\cdot \,\nabla \,v=0$
Notons $\beq {e_{u}}=\beq {e_{1}}$, $\beq {e_{v}}=\beq {e_{2}}$, $\beq {e_{w}}=\beq {e_{3}}$ et $\nabla \,u=\beq {e^{1}}$, $\nabla \,v=\beq {e^{2}}$, $\nabla \,w=\beq {e^{3}}$, les neufs produits scalaires précédents s’écrivent : $\beq {e_{i}}\,\cdot \,\beq {e^{j}}=\delta _{ij}$, ce qui montre que les systèmes de vecteurs {$\mathbf {e_{u}}$,$\mathbf {e_{v}}$,$\mathbf {e_{w}}$} et {$\nabla \,u$,$\nabla \,v$,$\nabla \,w$} constituent des systèmes réciproques.
On appelle coordonnées cylindro-paraboliques les paramètres $u,v,z$ définis par la transformation :
\begin{equation*}
x=(1/2)(u^{2}-v^{2})\,\,\,\,;\,\,\,\,y=u\,v\,\,\,\,;\,\,\,\,z=z\,\,\,\,\text{avec}\,\,\,\,-8<u<8\,\,\,,\,\,\,v\geqslant 0 \,\,\,\,et\,\,\,\,-8<z<8
\tag{4.4.28}
\end{equation*}
\begin{align*}
\beq{e_{u}} &= \dfrac{\partial\,x}{\partial\,u}\,\beq{i}+\dfrac{\partial\,y}{\partial\,u}\,\beq{j}+\dfrac{\partial\,z}{\partial\,u}\,\beq{k} = u\,\beq{i}+v\,\beq{j}\\
\beq{e_{v}} &= -v\,\beq{i}+u\,\beq{j}\\
\beq{e_{z}} &= \beq{k}
\tag{4.4.29}
\end{align*}
\begin{align*}
\beq{e_{u}}\,\cdot\,\beq{e_{v}} &= (u\,\beq{i}+v\,\beq{j})\,\cdot\,(-v\beq{i}+u\,\beq{j}) = -u\,v+u\,v=0\\
\beq{e_{u}}\,\cdot\,\beq{e_{z}} &= (u\,\beq{i}+v\,\beq{j})\,\cdot\,\beq{k} = 0\\
\beq{e_{v}}\,\cdot\,\beq{e_{z}} &= (-v\,\beq{i}+u\,\beq{j})\,\cdot\,\beq{k} = 0
\tag{4.4.30}
\end{align*}
\begin{equation*}
||\beq{e_{u}}||=\sqrt{u^{2}+v^{2}}\,\,\,\,;\,\,\,\,||\beq{e_{v}}||=\sqrt{u^{2}+v^{2}}\,\,\,\,;\,\,\,\,||\beq{e_{z}}||=1
\tag{4.4.31}
\end{equation*}
Déterminer les composantes covariantes $g_{ij}$ des tenseurs fondamentaux pour les systèmes de coordonnées suivants :
\begin{align*}
\beq{e_{1}} &= \dfrac{\partial\,\beq{M}}{\partial\,\rho} = \text{cos}\,\varphi\,\beq{i}+\text{sin}\,\varphi\,\beq{j}\\
\beq{e_{2}} &= \dfrac{\partial\,\beq{M}}{\partial\,\varphi} = -\rho\,\text{sin}\,\varphi\,\beq{i}+\rho\,\text{cos}\,\varphi\,\beq{j}\\
\beq{e_{3}} &= \dfrac{\partial\,\beq{M}}{\partial\,z} = \beq{k}
\tag{4.4.32}
\end{align*}
d’où : $g_{11}=1\,\,\,\,;\,\,\,\,g_{22}=\rho ^{2}\,\,\,\,;\,\,\,\,g_{33}=1$
\begin{align*}
\beq{e_{1}} &= \dfrac{\partial\,\beq{M}}{\partial\,u} = v\,\text{cos}\,\varphi\,\beq{i}+v\,\text{sin}\,\varphi\,\beq{j}-u\,\beq{k}\\
\beq{e_{2}} &= \dfrac{\partial\,\beq{M}}{\partial\,v} = u\,\text{cos}\,\varphi\,\beq{i}+u\,\text{sin}\,\varphi\,\beq{j}+v\,\beq{k}\\
\beq{e_{3}} &= \dfrac{\partial\,\beq{M}}{\partial\,\varphi} = -u\,v\,\text{sin}\,\varphi\,\beq{i}+u\,v\,\text{cos}\,\varphi\,\beq{j}
\tag{4.4.33}
\end{align*}
d’où : $g_{11}=v^{2}+u^{2}\,\,\,\,;\,\,\,\,g_{22}=v^{2}+u^{2}\,\,\,\,;\,\,\,\,g_{33}=u^{2}\,v^{2}$
\begin{align*}
\beq{e_{u}} &= \dfrac{\partial\,x}{\partial\,u}\,\beq{i}+\dfrac{\partial\,y}{\partial\,u}\,\beq{j}+\dfrac{\partial\,z}{\partial\,u}\,\beq{k} = u\,\beq{i}+v\,\beq{j}\\
\beq{e_{v}} &= -v\,\beq{i}+u\,\beq{j}\\
\beq{e_{z}} &= \beq{k}
\tag{4.4.34}
\end{align*}
d’où : $g_{11}=v^{2}+u^{2}\,\,\,\,;\,\,\,\,g_{22}=v^{2}+u^{2}\,\,\,\,;\,\,\,\,g_{33}=1$
Soient deux systèmes de coordonnées curvilignes : $u'^{i}=u'^{i}\,(u^{1},u^{2},...,u^{n})$ et $u^{j}=u^{j}\,(u'^{1},u'^{2},...,u'^{n})$. Écrire la loi de transformation des composantes mixtes $c^{mn}_{\,\,\,\,\,\,ijk}$ d’un tenseur, données dans le système de coordonnées $u^{j}$.
À tout changement de coordonnées curvilignes correspond un changement de base donné par les formules (4.3.16), soit :
\begin{equation*}
(a)\,\,\,\,A’^{k}_{i}=\partial_{i}\,u’^{k}\,\,\,\,;\,\,\,\,(b)\,\,\,\,A^{i}_{k}=\partial_{k}\,u^{i}
\tag{4.4.35}
\end{equation*}
La formule de transformation des composantes mixtes nous donne :
\begin{equation*}
c’^{pq}_{\,\,\,\,\,\,rst}=A’^{p}_{m}\,A’^{q}_{n}\,A^{i}_{r}\,A^{j}_{s}\,A^{k}_{t}\,c^{mn}_{ijk}=\partial_{m}\,u’^{p}\,\partial_{n}\,u’^{q}\,\partial_{r}\,u^{i}\,\partial_{s}\,u^{j}\,\partial_{t}\,u^{k}\,c^{mn}_{\,\,\,\,\,\,ijk}
\tag{4.4.36}
\end{equation*}
Soit $f(u^{1},u^{2},...,u^{n})$ une fonction dérivable par rapport aux $n$ variables $u^{i}$.
\begin{equation*}
u’^{i}=u’^{i}\,(u^{1},u^{2},...,u^{n})\,\,\,\,;\,\,\,\,u^{j}=u^{j}\,(u’^{1},u’^{2},...,u’^{n})
\tag{4.4.37}
\end{equation*}
La formule usuelle des dérivées partielles s’écrit :
\begin{equation*}
\dfrac{\partial\,f}{\partial\,u’^{i}}=\dfrac{\partial\,f}{\partial\,u^{j}}\,\partial_{i}\,u^{j}
\tag{4.4.38}
\end{equation*}
Au changement de coordonnées correspond un changement de base tel que : $\partial _{i}\,u^{j}=A^{j}_{i}$. Les dérivées $\partial \,f/\partial \,u'^{i}$ se transforment donc comme les composantes covariantes d’un tenseur d’ordre un. Cela justifie la notation $\partial _{i}\,f$ utilisée pour les dérivées partielles.
\begin{equation*}
\text{d}f=\partial_{i}\,f\,\text{d}u^{i}
\tag{4.4.39}
\end{equation*}
Les quantités $\text {d}u^{i}$ sont les composantes contravariantes d’un vecteur quelconque $\text {d}\beq {M}$. La quantité $\partial _{i}\,f\,\text {d}u^{i}$ apparaît comme le produit contracté des quantités $\partial _{i}\,f$ par $\text {d}u^{i}$ ; d’autre part, la différentielle $\text {d}f$ est un scalaire et, selon le critère général de tensorialité, les quantités $\partial _{i}\,f$ sont donc les composantes d’un tenseur d’ordre un. Le produit contracté est ici le produit scalaire du vecteur gradient par le vecteur $\text {d}\beq {M}$.
Soit un vecteur $\mathbf {X}$ de composantes covariantes $X_{i}$ ; $i=1$ à $n$.
\begin{equation*}
X_{i}=A’^{k}_{i}\,X’_{k}=\partial_{i}\,u’^{k}\,X’_{k}
\tag{4.4.40}
\end{equation*}
La dérivation de cette dernière expression nous donne :
\begin{equation*}
\dfrac{X_{i}}{\partial\,u^{j}}=\dfrac{X’_{k}}{\partial\,u^{j}}\,\partial_{i}\,u’^{k}+X’_{k}\,\partial_{ji}\,u’^{k}=\dfrac{X’_{k}}{\partial\,u’^{l}}\,\partial_{j}\,u’^{l}\,\partial_{i}\,u’^{k}+X’_{k}\,\partial_{ji}\,u’^{k}
\tag{4.4.41}
\end{equation*}
\begin{equation*}
\text{d}X_{i}=\partial_{i}\,u’^{k}\,\text{d}X’_{k}+X’^{k}\,\text{d}(\partial_{i}\,u’^{k})
\tag{4.4.42}
\end{equation*}
Les $\text {d}X_{i}$ ne se transforment pas comme les composantes d’un vecteur sauf dans le cas où les dérivées secondes $\partial _{ji}\,u'^{k}$ sont nulles.
On étudie l’interprétation géométrique de petites déformations d’un corps. Pour simplifier, on considère un système à deux dimensions formé par une feuille plane extensible. Soit $Ox_{1}x_{2}$ un référentiel cartésien fixe ; $P$ est un point de la feuille qui, après déformation, vient en $P'$ ; $Q$ est un autre point, voisin de $P$, qui vient en $Q'$ (Fig.4.3).
\begin{equation}
\text{d}u_{i}=\dfrac{\partial\,u_{i}}{\partial\,x_{j}}\,\text{d}x_{j}=e_{ij}\,\text{d}x_{j}\,\,\,\,;\,\,\,\,i,j=1,2
\tag{4.4.44}
\label{4.4.44}
\end{equation}
avec $e_{ij}=\partial \,u_{i}/\partial \,x_{j}$.
\begin{equation}
\text{d}u_{1}=e_{11}\,\text{d}x_{1}
\tag{4.4.45}
\label{4.4.45}
\end{equation}
Par conséquent, $e_{11}$ mesure l’allongement du matériau par unité de longueur, en chaque point $P$, dans la direction $Ox_{1}$. De même, $e_{22}$ représente l’allongement par unité de longueur dans le sens $Ox_{2}$.
\begin{equation}
\text{tan}\,\theta=\dfrac{\text{d}u_{2}}{\text{d}x_{1}+\text{d}u_{1}}
\tag{4.4.46}
\label{4.4.46}
\end{equation}
Comme on ne considère que de très faibles déformations, $u_{1}$ et $u_{2}$ sont petits par rapport à $x_{1}$ et $x_{2}$. On peut donc écrire :
\begin{equation}
\theta\simeq\dfrac{\text{d}u_{2}}{\text{d}x_{1}}=e_{21}
\tag{4.4.47}
\label{4.4.47}
\end{equation}
En conséquence, $e_{21}$ mesure l’angle de rotation de $PQ_{1}$, lors de la déformation. De même $e_{12}$ mesure l’angle de la rotation de $PQ_{2}$.
\begin{equation}
e_{11}=e_{22}=0\,\,\,\,;\,\,\,\,e_{12}=\varphi\,\,\,\,;\,\,\,\,e_{21}=-\varphi
\tag{4.4.48}
\label{4.4.48}
\end{equation}
Les composantes du tenseur $e_{ij}$ ne sont pas toutes nulles lors d’une rotation d’ensemble sans déformation ; on obtient alors un tenseur antisymétrique.
\begin{align}
\text{tenseur symétrique :}\,\,\,\,& S_{ij}=(1/2)\,(T_{ij}+T_{ji}) \notag \\
\text{tenseur antisymétrique :}\,\,\,\,& A_{ij}=(1/2)\,(T_{ij}-T_{ji})
\tag{4.4.49}
\label{4.4.49}
\end{align}
Le tenseur $T_{ij}$ s’écrit alors comme la somme :
\begin{equation}
T_{ij}=S_{ij}+A_{ij}
\tag{4.4.50}
\label{4.4.50}
\end{equation}
\begin{equation}
e_{ij}=\dfrac{e_{ij}+e_{ji}}{2}+\dfrac{e_{ij}-e_{ji}}{2}=S_{ij}+A_{ij}
\tag{4.4.51}
\label{4.4.51}
\end{equation}
On note que le tenseur calculé à la question (5) est antisymétrique et correspond à
une petite rotation d’ensemble. De manière générale, une rotation peut être
représentée par un vecteur axial qui équivaut à un tenseur antisymétrique de rang
deux.
La partie symétrique $S_{ij}$ du tenseur $e_{ij}$ donnée par (4.4.51) caractérise ainsi seulement la déformation. Sous forme développée, le tenseur $S_{ij}$ a pour matrice :
\begin{equation}
\begin{bmatrix}
S_{11}&S_{12}\\
S_{21}&S_{22}
\end{bmatrix}=\begin{bmatrix}
e_{11}&\dfrac{1}{2}\,(e_{12}+e_{21}) \\
\dfrac{1}{2}\,(e_{12}+e_{21}) & e_{22}
\end{bmatrix}
\tag{4.4.52}
\end{equation}
Les composantes situées sur la diagonale principale, $S_{11}$ et $S_{22}$, sont les allongements ou dilatations. Les composantes $S_{12}=S_{21}$ mesurent la déformation de cisaillement ou glissements.
La déformation d’une feuille plane extensible a été étudiée au cours de l’exercice précédent 4.11 dont nous reprenons les notations. Le tenseur des déformations pures comporte quatre composantes :
\begin{equation}
e_{11}=\epsilon_{1}\,\,\,\,;\,\,\,\,e_{22}=\epsilon_{2}\,\,\,\,;\,\,\,\,\dfrac{1}{2}\,(e_{12}+e_{21})=g_{1}=g_{2}
\tag{4.4.53}
\label{4.4.53}
\end{equation}
Si on se donne a priori quatre fonctions, celles-ci n’ont aucune raison de représenter les déformations d’un milieu continu. Par exemple, pour un tel milieu, des éléments initialement voisins doivent en effet le rester ; il ne peut également se produire de trous ou d’apports de matière ; etc. En conséquence, les composantes doivent vérifier entre elles des conditions de compatibilité qu’on va déterminer dans cet exercice.
\begin{equation}
A_{ij}=\dfrac{1}{2}\,(e_{ij}-e_{ji})\,\,\,\,;\,\,\,\,i,j=1,2
\tag{4.4.54}
\label{4.4.54}
\end{equation}
Écrire les dérivées partielles $\partial \,u_{2}/\partial \,x_{1}$ et $\partial \,u_{1}/\partial \,x_{2}$ en fonction des composantes $g_{1}$ et $A_{12}$.
\begin{equation}
\epsilon_{1}=\dfrac{\partial\,u_{1}}{\partial\,x_{1}}\,\,\,\,;\,\,\,\,\epsilon_{2}=\dfrac{\partial\,u_{2}}{\partial\,x_{2}}\,\,\,\,;\,\,\,\,g_{1}=g_{2}=\dfrac{1}{2}\,\bigg(\dfrac{\partial\,u_{2}}{\partial\,x_{1}}+\dfrac{\partial\,u_{1}}{\partial\,x_{2}}\bigg)
\tag{4.4.55}
\label{4.4.55}
\end{equation}
\begin{equation}
A_{11}=A_{22}=0\,\,\,\,;\,\,\,\,A_{12}=\dfrac{1}{2}\,\bigg(\dfrac{\partial\,u_{1}}{\partial\,x_{2}}-\dfrac{\partial\,u_{2}}{\partial\,x_{1}}\bigg)=-A_{21}
\tag{4.4.56}
\label{4.4.56}
\end{equation}
Combinant les relations (4.4.54) et (4.4.55), on obtient :
\begin{equation}
g_{1}+A_{12}=\dfrac{\partial\,u_{1}}{\partial\,x_{2}}\,\,\,\,;\,\,\,\,g_{1}-A_{12}=\dfrac{\partial\,u_{2}}{\partial\,x_{1}}
\tag{4.4.57}
\label{4.4.57}
\end{equation}
\begin{equation}
\dfrac{\partial^{2}\,u_{1}}{\partial\,x_{1}\,\partial\,x_{2}}=\dfrac{\partial\,\epsilon_{1}}{\partial\,x_{2}}=\dfrac{\partial\,g_{1}}{\partial\,x_{1}}+\dfrac{\partial\,A_{12}}{\partial\,x_{1}}\,\,\,\,;\,\,\,\,\dfrac{\partial^{2}\,u_{2}}{\partial\,x_{2}\,\partial\,x_{1}}=\dfrac{\partial\,\epsilon_{2}}{\partial\,x_{1}}=\dfrac{\partial\,g_{1}}{\partial\,x_{2}}-\dfrac{\partial\,A_{12}}{\partial\,x_{2}}
\tag{4.4.58}
\label{4.4.58}
\end{equation}
Dérivant les expressions (4.4.57) respectivement par rapport à $x_{1}$ et $x_{2}$, il vient :
\begin{equation}
\dfrac{\partial^{2}\,\epsilon_{1}}{\partial\,x_{2}^{2}}=\dfrac{\partial^{2}\,g_{1}}{\partial\,x_{2}\,\partial\,x_{1}}+\dfrac{\partial^{2}\,A_{12}}{\partial\,x_{2}\partial\,x_{1}}\,\,\,\,;\,\,\,\,\dfrac{\partial^{2}\,\epsilon_{2}}{\partial\,x_{1}^{2}}=\dfrac{\partial^{2}\,g_{1}}{\partial\,x_{1}\,\partial\,x_{2}}-\dfrac{\partial^{2}\,A_{12}}{\partial\,x_{1}\partial\,x_{2}}
\tag{4.4.59}
\label{4.4.59}
\end{equation}
La somme de ces deux dernières équations donne :
\begin{equation}
\dfrac{\partial^{2}\,\epsilon_{1}}{\partial\,x_{2}^{2}}+\dfrac{\partial^{2}\,\epsilon_{2}}{\partial\,x_{1}^{2}}=2\,\dfrac{\partial^{2}\,g_{1}}{\partial\,x_{2}\partial\,x_{1}}
\tag{4.4.60}
\label{4.4.60}
\end{equation}
C’est la condition de compatibilité des composantes du tenseur des déformations pour une feuille plane extensible.