Utiliser la convention de sommation pour écrire les expressions qui suivent ; préciser la valeur de $n$ dans chaque cas ainsi que les indices muets et libres.
\begin{equation*}
b_{jk}\,x_{k}=6 \,\,\,\,;\,\,\,\, n=3
\tag{1.6.1}
\end{equation*}
\begin{equation*}
b_{1j}\,d_{1j}=C \,\,\,\,;\,\,\,\, n=4
\tag{1.6.2}
\end{equation*}
Pour $n=3$, écrire explicitementl’expression $M_{ijk}\,B^{ij}$.
L’indice $k$ est un indice libre ; on a deux indices de sommation $i$ et $j$ et le nombre de termes obtenus doit être égal à $3^{2}=9$.
\[\begin {array}[b]{lclr} M_{ijk}^{ij}&=&M_{1jk}\,B^{1j}+M_{2jk}\,B^{2j}+M_{3jk}\,B^{3j}\\ &=&M_{11k}\,B^{11}+M_{12k}\,B^{12}+M_{13k}\,B^{13}+M_{21k}\,B^{21}+M_{22k}\,B^{22}+M_{23k}\,B^{23}\\ &+&M_{31k}\,B^{31}+M_{32k}\,B^{32}+M_{33k}\,B^{33} \end {array}\]
Démontrer les identités suivantes :
\begin{equation*}
a_{ij}\,x_{i}\,x_{j}=a_{ji}\,x_{j}\,x_{i}=a_{ji}\,x_{i}\,x_{j}
\tag{1.6.3}
\end{equation*}
\begin{equation*}
(a_{ik}-a_{ki})\,x_{i}\,x_{k}=a_{ik}\,x_{i}\,x_{k}-a_{ki}\,x_{i}\,x_{k}
\tag{1.6.4}
\end{equation*}
Utilisant le résultat précédent $a_{ij}\,x_{i}\,x_{j}=a_{ji}\,x_{i}\,x_{j}$, il vient :
\begin{equation*}
a_{ik}\,x_{i}\,x_{k}=a_{ki}\,x_{i}\,x_{k}
\tag{1.6.5}
\end{equation*}
d’où $(a_{ik}-a_{ki})\,x_{i}\,x_{k}=0$
Démontrer qu’un déterminant d’ordre trois peut s’écrire sous la forme :
\begin{equation*}
\text{det}\,[a_{ijk}]=\epsilon^{ijk}\,a_{1i}\,a_{2j}\,a_{3k}
\tag{1.6.6}
\end{equation*}
Développons l’expression, il vient :
\[\begin {array}[b]{lclr} \epsilon ^{ijk}\,a_{1i}\,a_{2j}\,a_{3k}&=&\epsilon ^{1jk}\,a_{11}\,a_{2j}\,a_{3k}+\epsilon ^{2jk}\,a_{12}\,a_{2j}\,a_{3k}+\epsilon ^{3jk}\,a_{13}\,a_{2j}\,a_{3k}\\ &=&a_{11}\,(\epsilon ^{1jk}\,a_{2j}\,a_{3k})+a_{12}\,(\epsilon ^{2jk}\,a_{2j}\,a_{3k})+a_{13}\,(\epsilon ^{3jk}\,a_{2j}\,a_{3k})\\ \end {array}\]
Les termes entre parenthèses sont les déterminants d’ordre deux. Le symbole d’antisymétrie $\epsilon ^{1jk}$ a pour valeur :
\begin{equation*}
\epsilon^{111}=\epsilon^{112}=\epsilon^{113}=\epsilon^{121}=\epsilon^{122}=\epsilon^{131}=\epsilon^{133}=0\,\,\,\,;
\,\,\,\,\epsilon^{123}=1\,\,\,;\,\,\,\,\epsilon^{132}=-1
\tag{1.6.7}
\end{equation*}
d’òu :
\begin{equation*}
\epsilon^{1jk}\,a_{2j}\,a_{3k}=a_{22}\,a_{33}-a_{23}\,a_{32}=\left| \begin{array}{cc}
a_{22} & a_{23} \\
\\
a_{32} & a_{33} \\
\end{array} \right |
\tag{1.6.8}
\end{equation*}
On obtient de même :
\begin{equation*}
\epsilon^{2jk}\,a_{2j}\,a_{3k}=a_{23}\,a_{31}-a_{21}\,a_{33}\,\,\,\,;\,\,\,\,\epsilon^{3jk}\,a_{2j}\,a_{3k}=a_{21}\,a_{32}-a_{22}\,a_{31}
\tag{1.6.9}
\end{equation*}
Regroupons avec le développement du début, on obtient :
\begin{equation*}
\epsilon^{ijk}\,a_{1i}\,a_{2j}\,a_{3k}=a_{11}\,\left| \begin{array}{cc}
a_{22} & a_{23} \\
\\
a_{32} & a_{33} \\
\end{array} \right | - a_{12}\,\,\left| \begin{array}{cc}
a_{21} & a_{23} \\
\\
a_{31} & a_{33} \\
\end{array} \right | + a_{13}\,\,\left| \begin{array}{cc}
a_{21} & a_{22} \\
\\
a_{31} & a_{32} \\
\end{array} \right |
\tag{1.6.10}
\end{equation*}
C’est l’expression du développement selon sa première ligne d’un déterminant d’ordre trois.
Considérons les vecteurs de base de $E_{3}$ :
\begin{equation*}
\beq{e_{1}}=(a,0,0)\,\,\,\,;\,\,\,\,\beq{e_{2}}=(b,c,0)\,\,\,\,;\,\,\,\,\beq{e_{3}}=(0,0,d)
\tag{1.6.11}
\end{equation*}
\begin{equation*}
\lambda_{1}\,\beq{e_{1}}+\lambda_{2}\,\beq{e_{2}}+\lambda_{3}\,\beq{e_{3}}=\lambda_{1}\,(a,0,0)+\lambda_{2}\,(b,c,0)+\lambda_{3}\,(0,0,d)=(0,0,0)
\tag{1.6.12}
\end{equation*}
On en déduit : $\lambda _{2}=\lambda _{3}=0$, d’où $\lambda _{1}=0$
Ces trois vecteurs sont linéairement indépendants et forment une base de $E_{3}$.
\begin{equation*}
\beq{X}=x^{1}\,\beq{e_{1}}+x^{2}\,\beq{e_{2}}+x^{3}\,\beq{e_{3}}
\tag{1.6.13}
\end{equation*}
Écrivons cette décomposition sous la forme suivante :
\begin{equation*}
\beq{X}=x^{1}\,(a,0,0)+x^{2}\,(b,c,0)+x^{3}\,(0,0,d)=(A,B,C)
\tag{1.6.14}
\end{equation*}
Identifiant les nombres correspondants entre eux, il vient :
\begin{equation*}
x^{1}\,a+x^{2}\,b=A\,\,\,;\,\,\,x^{2}\,c=B\,\,\,;\,\,\,x^{3}\,d=C
\tag{1.6.15}
\end{equation*}
d’où les valeurs des composantes :
\begin{equation*}
x^{1}=\dfrac{cA-bB}{ac}\,\,\,;\,\,\,x^{2}=\dfrac{B}{c}\,\,\,;\,\,\,x^{3}=\dfrac{C}{d}
\tag{1.6.16}
\end{equation*}
On considère trois vecteurs de $E_{3}$ :
\begin{equation*}
\beq{A}=(1,1,1)\,\,\,;\,\,\,\beq{B}=(0,1,1)\,\,\,;\,\,\,\beq{C}=(0,0,1)
\tag{1.6.17}
\end{equation*}
\begin{equation*}
\beq{e_{1}}\,\cdot\,\beq{e_{2}}=\beq{A}\,\cdot\,(\alpha\,\beq{A}+\beq{B})=0
\tag{1.6.18}
\end{equation*}
On obtient :
\begin{equation*}
\alpha=-\dfrac{\beq{A}\,\cdot\,\beq{B}}{\beq{A}\,\cdot\,\beq{A}}=-\dfrac{2}{3}
\tag{1.6.19}
\end{equation*}
Le vecteur $\mathbf {e_{2}}$ est égal à : $\beq {e_{2}}=-\dfrac {2}{3}\,\beq {A}+\beq {B}=(-\dfrac {2}{3},\dfrac {1}{3},\dfrac {1}{3})$
Le vecteur $\mathbf {e_{3}}$ est cherché sous la forme : $\beq {e_{3}}=\beta \,\beq {e_{1}}+\gamma \,\beq {e_{2}}+\beq {C}$. Écrivons les deux relations d’orthogonalité :
\begin{equation*}
\beq{e_{1}}\,\cdot\,\beq{e_{3}}=\beq{e_{1}}\,\cdot\,(\beta\,\beq{e_{1}}+\gamma\,\beq{e_{2}}+\beq{C})=0\,\,\,;\,\,\,\beq{e_{2}}\,\cdot\,\beq{e_{3}}=\beq{e_{2}}\,\cdot\,(\beta\,\beq{e_{1}}+\gamma\,\beq{e_{2}}+\beq{C})=0
\tag{1.6.20}
\end{equation*}
On obtient :
\begin{equation*}
\beq{e_{3}}=-\dfrac{1}{3}\,\beq{e_{1}}-\dfrac{1}{2}\,\beq{e_{2}}+\beq{C}=(0,-\dfrac{1}{2},\dfrac{1}{2})
\tag{1.6.21}
\end{equation*}
Soient deux vecteurs de $E_{3}$ :
\begin{equation*}
\beq{A}=(a_{1},a_{2},a_{3})\,\,\,\,;\,\,\,\,\beq{B}=(b_{1},b_{2},b_{3})
\tag{1.6.22}
\end{equation*}
et une base de $E_{3}$ définie par : {$\beq {e_{1}}=(1,1,1),\beq {e_{2}}=(0,1,1),\beq {e_{3}}=(0,0,1)$}
Calculer les valeurs numériques des composantes contravariantes et covariantes des vecteurs $\mathbf {A}$ et $\mathbf {B}$.
\begin{equation*}
\beq{A}=a_{1}\,\beq{e_{1}}+(a_{2}-a_{1})\,\beq{e_{2}}+(a_{3}-a_{2})\,\beq{e_{3}}\\
\tag{1.6.23}
\end{equation*}
\begin{equation*}
=x^{1}\,\beq{e_{1}}+x^{2}\,\beq{e_{2}}+x^{3}\,\beq{e_{3}}\\
\tag{1.6.24}
\end{equation*}
\begin{equation*}
\beq{B}=b_{1}\,\beq{e_{1}}+(b_{2}-b_{1})\,\beq{e_{2}}+(b_{3}-b_{2})\,\beq{e_{3}}\\
\tag{1.6.25}
\end{equation*}
\begin{equation*}
=y^{1}\,\beq{e_{1}}+y^{2}\,\beq{e_{2}}+y^{3}\,\beq{e_{3}}
\tag{1.6.26}
\end{equation*}
Par définition, les composantes contravariantes sont les nombres que multiplient les vecteurs de base. On a :
\begin{equation*}
x^{1}=a_{1}\,\,\,;\,\,\,x^{2}=a_{2}-a_{1}\,\,\,;\,\,\,x^{3}=a_{3}-a_{2}
\tag{1.6.27}
\end{equation*}
\begin{equation*}
y^{1}=b_{1}\,\,\,;\,\,\,y^{2}=b_{2}-b_{1}\,\,\,;\,\,\,y^{3}=b_{3}-b_{2}
\tag{1.6.28}
\end{equation*}
\begin{equation*}
x_{j}=A\,\cdot\,\beq{e_{j}}=(x^{1}\,\beq{e_{1}}+x^{2}\,\beq{e_{2}}+x^{3}\,\beq{e_{3}})\,\cdot\,\beq{e_{j}}\\
\tag{1.6.29}
\end{equation*}
\begin{equation*}
=x^{1}\,(\beq{e_{1}}\,\cdot\,\beq{e_{j}})+x^{2}\,(\beq{e_{2}}\,\cdot\,\beq{e_{j}})+x^{3}\,(\beq{e_{3}}\,\cdot\,\beq{e_{j}})\\
\tag{1.6.30}
\end{equation*}
\begin{equation*}
=x^{1}\,g_{1j}+x^{2}\,g_{2j}+x^{3}\,g_{3j}
\tag{1.6.31}
\end{equation*}
Les quantités $g_{ij}$ sont égales à $g_{ij}=\beq {e_{i}}\,\cdot \,\beq {e_{j}}$, soit :
\begin{equation*}
g_{11}=3\,\,\,;\,\,\,g_{12}=g_{21}=2\,\,\,;\,\,\,g_{13}=g_{31}=1
\tag{1.6.32}
\end{equation*}
\begin{equation*}
g_{22}=2\,\,\,;\,\,\,g_{23}=g_{32}=1\,\,\,;\,\,\,g_{33}=1
\tag{1.6.33}
\end{equation*}
Les composantes covariantes sont donc :
Vecteur $\mathbf {A}$ :
\begin{align*}
x_{1} &= a_{1}\,g_{11}+(a_{2}-a_{1})\,g_{21}+(a_{3}-a_{2})\,g_{31} = a_{1}+a_{2}+a_{3}\\
x_{2} &= a_{1}\,g_{12}+(a_{2}-a_{1})\,g_{22}+(a_{3}-a_{2})\,g_{32} = a_{2}+a_{3}\\
\tag{1.6.34}
\end{align*}
Vecteur $\mathbf {B}$ :
\begin{align*}
y_{1} &= b_{1}\,g_{11}+(b_{2}-b_{1})\,g_{21}+(b_{3}-b_{2})\,g_{31} = b_{1}+b_{2}+b_{3}\\
y_{2} &= b_{1}\,g_{12}+(b_{2}-b_{1})\,g_{22}+(b_{3}-b_{2})\,g_{32} = b_{2}+b_{3}\\
\tag{1.6.35}
\end{align*}
On peut également utiliser les expressions de définition des vecteurs pour calculer
les composantes covariantes. On a :
Vecteur $\mathbf {A}$ :
\begin{align*}
x_{1} &= \beq{A}\,\cdot\,\beq{e_{1}} = (a_{1},a_{2},a_{3})\,\cdot\,(1,1,1) = a_{1}+a_{2}+a_{3}\\
x_{2} &= \beq{A}\,\cdot\,\beq{e_{2}} = (a_{1},a_{2},a_{3})\,\cdot\,(0,1,1) = a_{2}+a_{3}\\
x_{3} &= \beq{A}\,\cdot\,\beq{e_{3}} = a_{3}\\
\tag{1.6.36}
\end{align*}
Vecteur $\mathbf {B}$ :
\begin{align*}
y_{1} &= \beq{B}\,\cdot\,\beq{e_{1}} = (b_{1},b_{2},b_{3})\,\cdot\,(1,1,1) = b_{1}+b_{2}+b_{3}\\
y_{2} &= \beq{B}\,\cdot\,\beq{e_{2}} = (b_{1},b_{2},b_{3})\,\cdot\,(0,1,1) = b_{2}+b_{3}\\
y_{3} &= \beq{B}\,\cdot\,\beq{e_{3}} = b_{3}\\
\tag{1.6.37}
\end{align*}
Composantes contravariantes :
Vecteur $\mathbf {A}$ : $x^{1}=4\,\,;\,\,x^{2}=-3\,\,;\,\,x^{3}=1\,\,$
Vecteur $\mathbf {B}$ : $y^{1}=1\,\,;\,\,y^{2}=2\,\,;\,\,y^{3}=2\,\,$
Composantes covariantes :
Vecteur $\mathbf {A}$ : $x_{1}=7\,\,;\,\,x_{2}=3\,\,;\,\,x_{3}=1\,\,$
Vecteur $\mathbf {B}$ : $y_{1}=9\,\,;\,\,y_{2}=8\,\,;\,\,y_{3}=5\,\,$
\begin{equation*}
\beq{A}\,\cdot\,\beq{B}=x^{1}\,y_{1}+x^{2}\,y_{2}+x^{3}\,y_{3}=17
\tag{1.6.38}
\end{equation*}
Soient deux systèmes de vecteurs réciproques, notés {$\beq {e_{1}},\beq {e_{2}},\beq {e_{3}}$} et {$\beq {e^{1}},\beq {e^{2}},\beq {e^{3}}$}. Partant de la définition des vecteurs réciproques : $\beq {e_{i}}\,\cdot \,\beq {e^{j}}=\delta _{ij}$,
\begin{equation*}
\beq{e^{1}}=\dfrac{\beq{e_{2}}\,\times\,\beq{e_{3}}}{V}\,\,\,;\,\,\,\beq{e^{2}}=\dfrac{\beq{e_{3}}\,\times\,\beq{e_{1}}}{V}\,\,\,;\,\,\,\beq{e^{3}}=\dfrac{\beq{e_{1}}\,\times\,\beq{e_{2}}}{V}\,\,\,\text{avec}\,\,\,V=\beq{e_{1}}\,\cdot\,(\beq{e_{2}}\,\times\,\beq{e_{3}})
\tag{1.6.39}
\end{equation*}
\begin{equation*}
\beq{e_{1}}=\dfrac{\beq{e^{2}}\,\times\,\beq{e^{3}}}{V}\,\,\,;\,\,\,\beq{e_{2}}=\dfrac{\beq{e^{3}}\,\times\,\beq{e^{1}}}{V}\,\,\,;\,\,\,\beq{e_{3}}=\dfrac{\beq{e^{1}}\,\times\,\beq{e^{2}}}{V}\,\,\,\text{avec}\,\,\,V’=\beq{e^{1}}\,\cdot\,(\beq{e^{2}}\,\times\,\beq{e^{3}})
\tag{1.6.40}
\end{equation*}
D’autre part : $\beq {e_{1}}\,\cdot \,\beq {e^{1}}=\lambda \,\beq {e_{1}}\,\cdot \,\,(\beq {e_{2}}\,\times \,\beq {e_{3}})=1$
d’où : $\lambda =\dfrac {1}{\beq {e_{1}}\,\cdot \,(\beq {e_{2}}\,\times \,\beq {e_{3}})}$ ; $\beq {e^{1}}=\dfrac {(\beq {e_{2}}\,\times \,\beq {e_{3}})}{\beq {e_{1}}\,\cdot \,(\beq {e_{2}}\,\times \,\beq {e_{3}})}$
On obtient de même :
$\beq {e^{2}}=\dfrac {(\beq {e_{3}}\,\times \,\beq {e_{1}})}{\beq {e_{1}}\,\cdot \,(\beq {e_{2}}\,\times \,\beq {e_{3}})}\,\,\,\,;\,\,\,\,\beq {e^{3}}=\dfrac {(\beq {e_{1}}\,\times \,\beq {e_{2}})}{\beq {e_{1}}\,\cdot \,(\beq {e_{2}}\,\times \,\beq {e_{3}})}$
On considère trois vecteurs formant une base orthogonale de $E_{3}$ :
\begin{equation*}
\beq{e_{1}}=(a,0,0)\,\,\,;\,\,\beq{e_{2}}=(0,b,0)\,\,;\,\,\beq{e_{3}}=(0,0,c)
\tag{1.6.41}
\end{equation*}
Déterminer la base réciproque.
\begin{equation*}
\beq{e_{i}}\,\cdot\,\beq{e^{j}}=\delta_{ij}
\tag{1.6.42}
\end{equation*}
Cherchons les vecteurs $\mathbf {e^{j}}$ sous la forme : $\beq {e^{j}}=(x_{j},y_{j},z_{j})$ ; la relation précédente nous donne :
\begin{equation*}
\beq{e_{1}}\,\cdot\,\beq{e^{1}}=(a,0,0)\,\cdot\,(x_{1},y_{1},z_{1})=a\,x_{1}=1 ;\\
\tag{1.6.43}
\end{equation*}
\begin{equation*}
\beq{e_{1}}\,\cdot\,\beq{e^{2}}=(a,0,0)\,\cdot\,(x_{2},y_{2},z_{2})=a\,x_{2}=0 ; \,\,\,\text{etc} \\
\tag{1.6.44}
\end{equation*}
Les vecteurs $\mathbf {e^{j}}$ de la base réciproque sont :
\begin{equation*}
\beq{e^{1}}=(\dfrac{1}{a},0,0)\,\,\,;\,\,\,\beq{e^{2}}=(0,\dfrac{1}{b},0)\,\,\,;\,\,\,\beq{e^{3}}=(0,0,\dfrac{1}{c})
\tag{1.6.45}
\end{equation*}
\begin{equation*}
||\beq{e_{1}}||=a\,\,\,;\,\,\,||\beq{e_{2}}||=b\,\,\,;\,\,\,||\beq{e_{3}}||=c
\tag{1.6.46}
\end{equation*}
Ceux de la base réciproque ont pour norme les inverses des grandeurs précédentes :
\begin{equation*}
||\beq{e^{1}}||=\dfrac{1}{a}=\dfrac{1}{||\beq{e_{1}}||}\,\,\,;\,\,\,||\beq{e^{2}}||=\dfrac{1}{b}=\dfrac{1}{||\beq{e_{2}}||}\,\,\,;\,\,\,||\beq{e^{3}}||=\dfrac{1}{c}=\dfrac{1}{||\beq{e_{3}}||}
\tag{1.6.47}
\end{equation*}
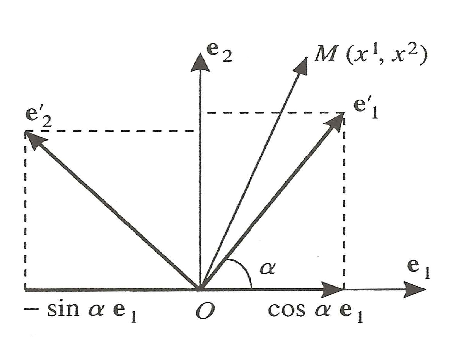
On considère dans un plan , un sytème d’axes orthogonaux portant les vecteurs $\mathbf {e_{1}}$ et $\mathbf {e_{2}}$ de longueur unité (Fig.1.3). Une rotation des axes dans le plan d’un angle $\alpha $, transforme ces vecteurs respectivement en $\mathbf {e'_{1}}$ et $\mathbf {e'_{2}}$.
\begin{equation*}
\beq{e’_{1}}=\text{cos}\,\alpha\,\beq{e_{1}}+\text{sin}\,\alpha\,\beq{e_{2}}
\tag{1.6.49}
\end{equation*}
\begin{equation*}
\beq{e’_{2}}=-\text{sin}\,\alpha\,\beq{e_{1}}+\text{cos}\,\alpha\,\beq{e_{2}}
\tag{1.6.50}
\end{equation*}
On obtient :
\begin{equation*}
A^{1}_{1}=\text{cos}\,\alpha\,\,\,;\,\,\,A^{2}_{1}=\text{sin}\,\alpha\,\,\,;\,\,\,A^{1}_{2}=-\text{sin}\,\alpha\,\,\,;\,\,\,A^{2}_{2}=\text{cos}\,\alpha
\tag{1.6.51}
\end{equation*}
\begin{equation*}
\beq{e_{1}}=\text{cos}\,\alpha\,\beq{e’_{1}}-\text{sin}\,\alpha\,\beq{e’_{2}}
\tag{1.6.52}
\end{equation*}
\begin{equation*}
\beq{e_{2}}=\text{sin}\,\alpha\,\beq{e’_{1}}+\text{cos}\,\alpha\,\beq{e’_{2}}
\tag{1.6.53}
\end{equation*}
On obtient :
\begin{equation*}
A’^{1}_{1}=\text{cos}\,\alpha\,\,\,;\,\,\,A’^{2}_{1}=-\text{sin}\,\alpha\,\,\,;\,\,\,A^{’1}_{2}=\text{sin}\,\alpha\,\,\,;\,\,\,A’^{2}_{2}=\text{cos}\,\alpha
\tag{1.6.54}
\end{equation*}
\begin{equation*}
\beq{OM}=x^{1}\,\beq{e_{1}}+x^{2}\,\beq{e_{2}}=(x^{1}\,\text{cos}\,\alpha+x^{2}\,\text{sin}\,\alpha)\,\beq{e’_{1}}+(-x^{1}\,\text{sin}\,\alpha+x^{2}\,\text{cos}\,\alpha)\,\beq{e’_{2}}
\tag{1.6.55}
\end{equation*}
\begin{equation*}
=x’^{1}\,\beq{e’_{1}}+x’^{2}\,\beq{e’_{2}}
\tag{1.6.56}
\end{equation*}
Identifiant les composantes entre elles, il vient :
\begin{equation*}
x’^{1}=x^{1}\,\text{cos}\,\alpha+x^{2}\,\text{sin}\,\alpha\,\,\,;\,\,\,;x’^{2}=-x^{1}\,\text{sin}\,\alpha+x^{2}\,\text{cos}\,\alpha
\tag{1.6.57}
\end{equation*}
Un calcul similaire nous donne :
\begin{equation*}
x^{1}=x’^{1}\,\text{cos}\,\alpha-x’^{2}\,\text{sin}\,\alpha\,\,\,;\,\,\,;x^{2}=x’^{1}\,\text{sin}\,\alpha+x’^{2}\,\text{cos}\,\alpha
\tag{1.6.58}
\end{equation*}
Vérifions la formule (1.3.16), par exemple, on a : $x'^{k}=A'^{k}_{i}\,x^{i}$ soit :
\begin{equation*}
x’^{1}=x^{1}\,A’^{1}_{1}+x^{2}\,A’^{1}_{2}=x^{1}\,\text{cos}\,\alpha+x^{2}\,\text{sin}\,\alpha
\tag{1.6.59}
\end{equation*}
\begin{equation*}
x’^{2}=x^{1}\,A’^{2}_{1}+x^{2}\,A’^{2}_{2}=-x^{1}\,\text{sin}\,\alpha+x^{2}\,\text{cos}\,\alpha
\tag{1.6.60}
\end{equation*}