1 : Triplets de nombres - Considérons l’exemple des vecteurs constitués
par ds triplets de nombres. Soit la base de $E_{3}$ formée des vecteurs $\beq {e_{1}}=(1,0,0)$, $\beq {e_{2}}=(0,1,0)$, $\beq {e_{3}}=(0,0,1)$ et deux
vecteurs quelconques de cet espace vectoriel décomposés sur cette base : $\beq {x}=x^{i}\,\beq {e_{i}}$ et
$\beq {y}=y^{i}\,\beq {e_{i}}$.
Par définition, le produit scalaire des vecteurs $\mathbf {x}$ et $\mathbf {y}$ est le nombre, noté $\beq {x}\cdot \beq {y}$, donné
par :
\begin{equation}
\beq{x}\cdot \beq{y}=x^{1}\,y^{1}+x^{2}\,y^{2}+x^{3}\,y^{3}=x^{i}\,y^{i}
\tag{1.4.1}
\label{1.4.1}
\end{equation}
On vérifie aisément que le produit scalaire ainsi défini possède les propriétés
suivantes :
1) $\beq {x}\,\cdot \,\beq {y}=\beq {y}\,\cdot \,\beq {x}$ ; 2) $(\beq {x}+\beq {y})\,\cdot \,\beq {z}=\beq {x}\,\cdot \,\beq {z}+\beq {y}\,\cdot \,\beq {z}$ ; 3) $(\lambda \beq {x})\,\cdot \,\beq {y}=\lambda (\beq {x}\,\cdot \,\beq {y})$ ; 4) Pour tout vecteur donné $\mathbf {x}$, si l’on a $\beq {x}\,\cdot \,\beq {y} =0$ pour tout vecteur $\mathbf {y}$ de $E_{3}$, alors
$\beq {x}=\beq {0}$.
2 : Polynômes - Considérons l’espace vectoriel des polynômes $P_{a}(x)$ de degré deux. On peut définir, par exemple, un produit scalaire des polynômes entre eux par l’intégrale suivante :
\begin{equation}
P_{a}(x)\cdot P_{b}(x)=\mathlarger{\int}_{-1}^{+1}\,P_{a}(x)\,P_{b}(x)\,dx
\tag{1.4.2}
\label{1.4.2}
\end{equation}
On vérifie aisément qu’un tel produit scalaire possède également les propriétés précďentes.
Le produit scalaire de deux vecteurs quelconques est défini de manière générale à partir
de ses propriétés.
On appelle produit scalaire une loi de composition qui, à tout couple, de vecteurs $\mathbf {x}$,$\mathbf {y}$ d’un
espace vectoriel $E_{n}$, associe un nombre réel, souvent noté $\beq {x}\cdot \beq {y}$, et vérifie les axiomes
suivants :
Un espace vectoriel sur lequel on a défini un produit scalaire est appelé un espace vectoriel pré-euclidien.
Considérons un espace vectoriel pré-euclidien $E_{n}$ rapporté à une base quelconque ($\mathbf {e_{i}}$). Les vecteurs de $E_{n}$ s’écrivent sur cette base : $\beq {x}=x^{i}\,\beq {e_{i}}$, $\beq {y}=y^{j}\,\beq {e_{j}}$. Le produit scalaire, compte tenu des propriétés PS2 et PS3, s’écrit :
\begin{equation}
\beq{x}\cdot\beq{y}=(x^{i}\,\beq{e_{i}})\cdot(y^{j}\,\beq{e_{j}})=x^{i}\,y^{j}\,(\beq{e_{i}}\cdot\beq{e_{j}})=g_{ij}\,x^{i}\,y^{j}
\tag{1.4.3}
\label{1.4.3}
\end{equation}
avec $g_{ij}=\beq {e_{i}}\,\cdot \,\beq {e_{j}}$. On obtient donc l’expression générale du produit scalaire sous la forme :
\begin{equation}
\beq{x}\cdot\beq{y}=g_{ij}\,x^{i}\,y^{j}
\tag{1.4.4}
\label{1.4.4}
\end{equation}
La donnée des $g_{ij}$ correspond à la définition même du produit scalaire
particulier que l’on se donne sur un espace vectoriel. Ces quantités ne peuvent
cependant pas être entièrement arbitraires car, réciproquement, l’expression
(1.4.4) du produit scalaire de deux vecteurs doit vérifier les propriétés PS1 à
PS4.
Pour satisfaire la propriété de commutativité (PS1), on doit avoir :
\begin{equation}
\beq{x}\cdot\beq{y}=g_{ij}\,x^{i}\,y^{j}=\beq{y}\cdot\beq{x}=g_{ji}\,y^{j}\,x^{i}
\tag{1.4.5}
\label{1.4.5}
\end{equation}
d’òu : $g_{ij}=g_{ji}$.
D’autre part, la propriété PS4 nécessite que si $g_{ij}\,x^{i}\,y^{j}=0$ pour tous $y^{j}$, alors on doit avoir : $x^{i}=0$. Or, l’égalité $g_{ij}\,x^{i}\,y^{j}=0$ est vérifiée, pour des valeurs arbitraires de $y^{j}$, seulement si l’on a : $g_{ij}\,x^{i}=0$. Ce système de $n$ équations à $n$ inconnues ne devant admettre par hypothèse que la solution $x^{i}=0$, il faut et il suffit pour cela que le déterminant, noté $g$, du système soit différent de zéro ; on doit donc avoir :
\begin{equation}
g=\text{det}\,[g_{ij}]\neq\,0
\tag{1.4.6}
\label{1.4.6}
\end{equation}
Deux vecteurs $\mathbf {x}$ et $\mathbf {y}$, non nuls, d’un espace pré-euclidien sont dits orthogonaux entre eux lorsque leur produit scalaire est nul, soit :
\begin{equation}
\beq{x}\cdot\beq{y}=0
\tag{1.4.7}
\end{equation}
Un système de $n$ vecteurs $\mathbf {x_{i}}$, tous orthogonaux entre eux, constitue un système
orthogonal.
Si l’on choisit des vecteurs orthogonaux linéairement indépendants en nombre égal à
la dimension de l’espace vectoriel, ce système de vecteurs constitue une base de cet
espace. Cette base est appelée une base orthogonale. Nous allons montrer qu’il
est toujours possible de déterminer une base orthogonale d’un espace vectoriel
pré-euclidien.
Remarque - Dans un espace pré-euclidien, des vecteurs orthogonaux peuvent être linéairement dépendants. Considérons par exemple des vecteurs $\beq {x}=x^{i}\,\beq {e_{i}}$ et $\beq {y}=y^{j}\,\beq {e_{j}}$ d’un espace vectoriel à deux dimensions et définissons leur produit scalaire par :
\begin{equation}
\beq{x}\cdot\beq{y}=x^{1}\,y^{1}-x^{2}\,y^{2}
\tag{1.4.8}
\end{equation}
Si l’on considère, par exemple, les deux vecteurs $\beq {x}=\beq {e_{1}}+\beq {e_{2}}$ et $\beq {y}=\alpha (\beq {e_{1}}+\beq {e_{2}})$, qui sont linéairement dépendants, on obtient $\beq {x}\cdot \beq {y}=0$. Pour un tel produit scalaire, les vecteurs $\beq {y}=\alpha (\beq {e_{1}}+\beq {e_{2}})$ sont tels que $\beq {y}\cdot \beq {y}=0$.
La méthode dite d’orthogonalisation de Schmidt permet le calcul effectif d’une base
orthogonale pour tout espace vectoriel pré-euclidien $E_{n}$.
Pour cela, considérons un ensemble de $n$ vecteurs linéairement indépendants $(\beq {x_{1}},\beq {x_{2}},...,\beq {x_{n}})$ de $E_{n}$ et
supposons que l’on ait, pour chaque vecteur : $\beq {x_{i}}\cdot \beq {x_{i}}\neq 0$. Cherchons $n$ vecteurs $\mathbf {e_{i}}$ orthogonaux entre
eux.
Partons de $\beq {e_{1}}=\beq {x_{1}}$ et cherchons $\mathbf {e_{2}}$ orthogonal à $\mathbf {e_{1}}$, sous la forme : \begin{equation}
\beq{e_{2}}=\lambda_{1}\beq{e_{1}}+\beq{x_{2}}
\tag{1.4.9}
\end{equation}
Le coefficient $\lambda _{1}$ se calcule en écrivant la relation d’orthogonalité :
\begin{equation}
\beq{e_{1}}\,\cdot\,\beq{e_{2}}=\beq{x_{1}}\,\cdot\,(\lambda_{1}\beq{x_{1}}+\beq{x_{2}})=0
\tag{1.4.10}
\end{equation}
On en déduit : $\lambda _{1}=-(\beq {x_{1}}\,\cdot \,\beq {x_{2}})/(\beq {x_{1}})^{2}$. Le paramètre $\lambda _{1}$ étant déterminé, on obtient le vecteur $\mathbf {e_{2}}$ qui est
orthogonal à $\mathbf {e_{1}}$ et non nul puisque le système $(\beq {e_{1}},\beq {x_{2}},...,\beq {x_{n}})$ est linéairement indépendant.
Le vecteur suivant $\mathbf {e_{3}}$ est cherché sous la forme :
\begin{equation}
\beq{e_{3}}=\mu_{1}\beq{e_{1}}+\mu_{2}\beq{e_{2}}+\beq{x_{3}}
\tag{1.4.11}
\end{equation}
Les deux relations d’orthogonalité : $\beq {e_{1}}\cdot \beq {e_{2}}=0$ et $\beq {e_{2}}\cdot \beq {e_{3}}=0$, permettent le calcul des coefficients $\mu _{1}$ et $\mu _{2}$. On obtient :
\begin{equation}
\mu_{1}=-(\beq{e_{1}}\cdot\beq{x_{3}})/(\beq{e_{1}})^{2}\,\,\, ;\,\,\, \mu_{2}=-(\beq{e_{2}}\cdot\beq{x_{3}})/(\beq{e_{2}})^{2}
\tag{1.4.12}
\end{equation}
ce qui détermine le vecteur $\mathbf {e_{2}}$ orthogonal à $\mathbf {e_{1}}$ et $\mathbf {e_{2}}$, et non nul puisque le système $(\beq {e_{1}},\beq {e_{2}},\beq {x_{3}},...,\beq {x_{n}})$
est indépendant. En continuant le même type de calcul, on obtient de proche
en proche un système de vecteurs $(\beq {e_{1}},\beq {e_{2}},...,\beq {e_{n}})$ orthogonaux entre eux et dont aucun n’est
nul.
Dans le cas où certains vecteurs seraient tels que $\beq {x_{i}}\,\cdot \,\beq {x_{i}}=0$, on remplace $\mathbf {x_{i}}$ par $\beq {x'_{i}}=\beq {x_{i}}+\lambda \,\beq {x_{j}}$ en choisissant un
vecteur $\mathbf {x_{j}}$ de telle sorte que l’on obtienne $\beq {x'_{i}}\,\cdot \,\beq {x'_{i}}\neq 0$.
On en déduit donc que tout espace vectoriel pré-euclidien admet des bases
orthogonales.
Produit scalaire sur une base orthogonale - Lorsque les vecteurs de base $(\beq {e_{1}},\beq {e_{2}},...,\beq {e_{n}})$ d’un espace vectoriel sont orthogonaux, les quantités :
\begin{equation}
g_{ij}=\beq{e_{i}}\,\cdot\,\beq{e_{j}}
\tag{1.4.13}
\end{equation}
sont nulles si $i\neq j$. Le produit scalaire de deux vecteurs $\mathbf {x}$ et $\mathbf {y}$, décomposés sur cette base, se réduit alors à :
\begin{equation}
\beq{x}\,\cdot\,\beq{y}=g_{11}\,x^{1}\,y^{1}+g_{22}\,x^{2}\,y^{2}+...+g_{nn}\,x^{n}\,y^{n}
\tag{1.4.14}
\label{1.4.14}
\end{equation}
De manière générale, les quantités $g_{ij}$ peuvent être positives ou négatives.
Le produit scalaire d’un vecteur $\mathbf {x}$ peut permettre de définir la notion de norme d’un vecteur. On a pour le carré de la norme :
\begin{equation}
\beq{x}\,\cdot\,\beq{x}=g_{ij}\,x^{i}\,x^{j}=(\mathrm{norme}\,\,\beq{x})^{2}=\|\beq{x}\|^{2}
\tag{1.4.15}
\label{1.4.15}
\end{equation}
Les nombres $g_{ij}$ définissent en quelque sorte une "mesure" des vecteurs ; on dit qu’ils
constituent la métrique de l’espace vectoriel.
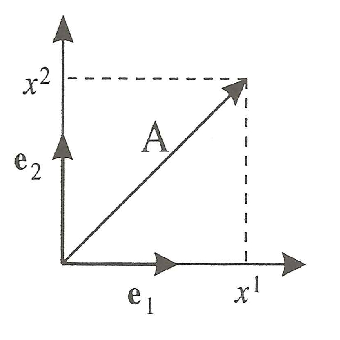
Exemple - En géométrie classique, la norme représente la longueur d’un vecteur
(Fig.1.1). Considérons un plan et des vecteurs de base $\beq {e_{1}}=(1,0)$ et $\beq {e_{2}}=(0,1)$, avec $g_{ij}=\delta _{ij}$. Soit un vecteur $\beq {A}=x^{1}\,\beq {e_{1}}+x^{2}\,\beq {e_{2}}$ ; on a :
\begin{equation}
\|\beq{A}\|=(\beq{A}\,\cdot\,\beq{A})^{1/2}=[(x^{1})^{2}+(x^{2})^{2}]^{1/2}
\tag{1.4.16}
\end{equation}
Signature d’un espace vectoriel - Dans l’espace de la géométrie classique, la norme
est un nombre qui est toujours strictement positif et qui ne devient nul que si le vecteur
est égal à zéro. Par contre l’expression (1.4.15) de la norme d’un vecteur, peut être
éventuellement négative pour des nombres $g_{11},g_{12},...,g_{nn}$ quelconques. On peut donc distinguer deux
genres d’espaces vectoriels pré-euclidiens selon que la norme est positive ou
non.
Considérons une base orthogonale ($\mathbf {e_{i}}$) d’un espace pré-euclidien $E_{n}$, ce qui est toujours
possible. Le carré de la norme d’un vecteur s’écrit alors, en faisant $\beq {y}=\beq {x}$ dans l’expression
(1.4.14) :
\begin{equation}
(\mathrm{norme}\,\,\beq{x})^{2}=\beq{x}\,\cdot\,\beq{x}=g_{11}\,(x^{1})^{2}\,+g_{22}\,(x^{2})^{2}\,+,...,+g_{nn}\,(x^{n})^{2}
\tag{1.4.18}
\label{1.4.18}
\end{equation}
Les nombres $g_{ij}$ pouvant être négatifs ou positifs, la norme d’un vecteur comporte une
série de signe + et -, la valeur zéro étant interdite par suite de la relation (1.4.6) :
$g=d\acute {e}t\,[g_{ij}]\neq \,0$.
Le nombre de signes + et de signes - constitue une caractéristique d’un espace vectoriel
donné $E_{n}$ ; elle est appelée la signature de l’espace vectoriel $E_{n}$. Cette signature
est une propriété intrinsèque de l’espace $E_{n}$ ; elle ne dépend donc pas de la base
considérée.