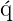uence de l’hypothèse (2) ci-dessus.
Les notions classiques de systèmes de coordonnées peuvent être généralisées à des
espaces ponctuels à $n$ dimensions. On appelle système de coordonnées dans $\varepsilon _{n}$, tout mode de
définition d’un point $M$ de cet espace en fonction de $n$ scalaires $u^{i}$ qui sont appelées
coordonnées de $M$ dans le système considéré.
Par exemple, dans l’espace $\varepsilon _{3}$ de la géométrie ordinaire, les coordonnées sont des
scalaires généralement notés $x$, $y$, $z$. Le système de coordonnées sphériques comporte trois
paramètres notés $r$, $\theta $, $\varphi $.
Pour un système donné de coordonnées, on appelle ligne coordonnée le lieu des
points $M$ lorsqu’une seule coordonnée varie, les autres étant égales à des constantes. En un
point $M$ donné se croisent $n$ lignes coordonnées.
Ainsi dans l’espace $\varepsilon _{3}$, rapporté à un repère fixe, on obtient des lignes coordonnées qui
sont des droites lorsque l’on pose, par exemple, $y=$cte, $z=$cte et que l’on fait varier
$x$.
Étudions tout d’abord la généralisation d’un système de coordonnées relatives à un
repère fixe.
Les lignes coordonnées sont dans ce cas des droites et pour cette raison, ces coordonnées sont appelées des coordonnées rectilignes.
Considérons, à titre d’exemple, un système de coordonnées de l’espace $\varepsilon _{3}$, de la géométrie ordinaire. Les points de cet espace peuvent être repérés à l’aide d’un système de coordonnées $u^{1}$, $u^{2}$, $u^{3}$, appelées coordonnées sphériques, celles-ci étant généralement notées $u^{1}=r$, $u^{2}=\theta $, $u^{3}=\varphi $. Ces coordonnées sont définies à partir d’un repère fixe cartésien de $\varepsilon _{3}$, que l’on va noter $(O,\beq {i},\beq {j},\beq {k})$ et les coordonnées rectilignes d’un point $M$ de $\varepsilon _{3}$ sont notées $x^{i}$,$i=1,2,3$. Les coordonnées sphériques sont définies par les relations suivantes :
\begin{equation}
x^{1}=r\,\text{sin}\,\theta\,\text{cos}\,\varphi\,\,\,\,;\,\,\,\,x^{2}=r\,\text{sin}\,\theta\,\text{sin}\,\varphi\,\,\,\,;\,\,\,\,x^{3}=r\,\text{cos}\,\theta
\tag{4.2.1}
\label{4.2.1}
\end{equation}
Les lignes coordonnées sont obtenues en maintenant constant deux paramètres et en
faisant varier le troisième. Pour $r$ variable, on obtient des droites passant par le point $O$
et dont la direction est déterminée par les valeurs fixées des angles $\theta $ et $\varphi $. Les
variations de $\theta $ font décrire au point $M$ un cercle centré sur $O$, de rayon $r$ et situé dans le
plan défini par l’angle $\varphi $. Les variations de $\varphi $ donnent un cercle centré sur l’axe $Ox^{3}$ et
situé dans un plan parallèle au plan $x^{1}O x^{2}$. En un point donné se croisent trois lignes
coordonnées.
Les coordonnées rectilignes $x^{i}$ sont des fonctions $x^{i}(r,\theta ,\varphi )$ continûment dérivables par rapport aux coordonnées $r$, $\theta $, $\varphi $ (sauf pour $x^{1}=x^{2}=0$). Le jacobien de la transformation est différent de zéro, ce qui assure la biunivocité de la correspondance entre un point $M$ et ses coordonnées sphériques. On obtient inversement les relations :
\begin{equation}
\begin{array}[b]{ll}
&r=\big[(x^{1})^{2}+(x^{2})^{2}+(x^{3})^{2}\big]^{1/2}\,\,\,\,;\,\,\,\,\varphi=\text{arctan}\,(x^{2}/x^{1})\\
&\theta=\text{arcos}\bigg(\dfrac{x^{3}}{\big[(x^{1})^{2}+(x^{2})^{2}+(x^{3})^{2}\big]^{1/2}}\bigg)
\end{array}
\tag{4.2.2}
\label{4.2.2}
\end{equation}
Les coordonnées sphériques constituent un exemple de système de coordonnées dites curvilignes dans l’espace $\varepsilon _{3}$ (valables seulement sur l’espace privé d’une droite).
Considérons à présent un espace ponctuel $\varepsilon _{n}$ et un repère $(O,\beq {e^{0i}})$ de cet espace. Soit $x^{i}$ les
coordonnées rectilignes d’un point $M$ de $\varepsilon _{n}$ par rapport à ce repère.
Un système de coordonnées quelconques $u^{k}$, $k=1$ à $n$, est obtenu en se donnant $n$ fonctions arbitraires $f^{i}$ des paramètres $u^{k}$, telles que :
\begin{equation}
x^{i}=f^{i}(u^{1},u^{2},...,u^{n});\,\,\,\,i=1,...,n
\tag{4.2.3}
\label{4.2.3}
\end{equation}
On supposera par la suite que les $n$ fonctions $f^{i}$ satisfont aux propriétés suivantes :
1- Elles sont continûment dérivables jusqu’à un certain ordre supérieur ou égal à 2. Cette hypothèse implique, en tout point où elle est est satisfaite, que l’on a la permutabilité des dérivations :
\begin{equation}
\partial_{kl}\,f^{i}=\partial_{lk}\,f^{i}
\tag{4.2.4}
\label{4.2.4}
\end{equation}
2- Ces fonctions sont telles qu’on peut résoudre le système de $n$ équations (4.2.3) par rapport aux variables $u^{k}$ et les exprimer en fonction des $x^{i}$, soit :
\begin{equation}
u^{k}=g^{k}(x^{1},x^{2},...,x^{n});\,\,\,\,k=1,...,n
\tag{4.2.5}
\label{4.2.5}
\end{equation}
3- Lorsque les variables $u^{k}$ varient dans un domaine $\Delta $, les variables $x^{i}$ varient dans un domaine $\Delta '$. Le jacobien des fonctions $x^{i}=f^{i}(u^{1},u^{2},...,u^{n})$, donné par :
\begin{equation}
D(\partial_{k}\,x^{i})=\begin{bmatrix}
\partial_{1}\,x^{1}&\partial_{1}\,x^{2}&...&\partial_{1}\,x^{n} \\
\partial_{2}\,x^{1}&\partial_{2}\,x^{2}&...&\partial_{2}\,x^{n} \\
...&...&...&...\\
\partial_{n}\,x^{1}&\partial_{n}\,x^{2}&...&\partial_{n}\,x^{n}
\end{bmatrix}
\tag{4.2.6}
\label{4.2.6}
\end{equation}
sera supposé différent de zéro dans le domaine $\Delta $ ainsi que le jacobien $D(\partial _{i}\,u^{k})$ des fonctions $u^{k}=g^{k}(x^{1},x^{2},...,x^{n})$
qui est l’inverse du jacobien $D(\partial _{k}\,x^{i})$. Si les jacobiens existent, ils sont non nuls comme cons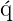uence de l’hypothèse (2) ci-dessus.
Si l’on fixe $(n-1)$ paramètres $u^{k}$ en faisant varier un seul paramètre, $u^{1}$ par exemple, on obtient les coordonnées $x^{i}_{(1)}$ d’un ensemble de points $M$ de $\varepsilon _{n}$ qui constituent une ligne coordonnée. En général, les lignes coordonnées ne sont pas des droites mais des courbes ; ces coordonnées $u^{k}$ sont appelées pour cette raison des coordonnées curvilignes. En un point $M$ de $\varepsilon _{n}$ se croisent $n$ lignes coordonnées.