DOURNAC.ORG
Français  English

Sciences > Energy calibration of calorimeter in NEMO3 experiment

Remerciements

  • Je tiens à remercier sincèrement mon tuteur de stage Roger Arnold ainsi que tout le groupe NEMO présent au sein de l'IReS (Christine Marquet, Vera Kovalenko et Victor Tretiak) pour leur disponibilité, leur gentillesse et toute l'aide qu'ils m'ont apportée au cours de ce stage.

    Je tiens à remercier aussi tout particulièrement Lotfi pour nos discussions animées et sa constante bonne humeur.

    J'adresse enfin mes remerciements aux autres étudiants de l'IReS qui ont rendu ce stage très plaisant.

Résumé

Calibrage en énergie du calorimètre dans l'expérience NEMO3

La collaboration NEMO (France, Russie, Rép. Tchèque, Japon, Etats-Unis) a lancé depuis Juillet 2002 l'expérience NEMO3 qui vise à mettre en évidence la désintégration double $ \beta$ sans émission de neutrinos correspondant à l'émission simultannée de 2 électrons dont la somme en énergie est égale à l'énergie de transition. L'objectif est de pouvoir confirmer la nature Majorana du neutrino avec une sensibilité de 0.1 eV sur sa masse effective au bout de 5 ans de prises de données. Une telle sensibilité nécessite une maîtrise du bruit de fond et un suivi rigoureux de l'étalonnage en énergie et en temps. La collaboration prévoit deux niveaux de contrôle: un calibrage absolu en énergie utilisant des sources radioactives adaptées pour une calibration jusqu'à 3.5 MeV qui sera effectué 1 à 2 fois par an et un calibrage journalier à l'aide d'un système laser. Nous présentons ici, à la suite des acquisitions de données effectuées sur le détecteur NEMO3 en Avril 2002, la méthode employée et les résultats donnés par ce premier test sans blindage neutron sur l'étalonnage absolu en énergie du calorimètre. La résolution obtenue sans la totalité du blindage ($ \sigma$=70 keV à 1 MeV) résulte de conditions de prises de données relativement mauvaises. Nos résultats de calibrage sont cependant validés par l'utilisation des corrections issues du système laser. Nous avons testé, en estimant la résolution spatiale sur la localisation des points d'émission obtenue avec la chambre à fils, la capacité de la chaîne d'acquisition à sélectionner les événements propres au calibrage. Une légère dissymétrie dans la reconstruction longitudinale des vertex nous indiquent un défaut dans l'algorithme utilisé. L'assemblage du détecteur est maintenant achevé depuis l'installation du blindage complet (fer et blindage neutron) et une autre séance de calibrage est prévue pour l'été 2002.

Abstract

Energy calibration of calorimeter in NEMO3 experiment

The NEMO collaboration (France, Russia, Czesch. Rep, Japan, USA) has launched since July 2002 the NEMO3 experiment whose goal is the investigation of double-beta decay without neutrino emission corresponding to the simultaneous emission of two electrons with an energy equal to the decay energy. This process, if it can be observed, would confirm the Majorana nature of neutrino. The collaboration is looking to measure the effective Majorana neutrino mass with a sensitivity in the order of 0.1 eV after 5 years. This constraint implies a good knowledge of background and a reliable monitoring on energy and time calibration. During data acquisition, the collaboration intends to put two monitoring levels: on the first hand, an absolute calibration performed one or two times a year using relevant radioactive sources for a calibration up to 3.5 MeV, and on the other, a daily tracking with a laser system. Following to the data collection carried out on the NEMO3 detector during April 2002, we present here the method used and the results obtained concerning this first test without neutron shielding for the absolute energy calibration of the NEMO3 calorimeter. The resolution obtained without a full shield (FWHM=17%) is not significant because of relatively bad collection conditions. However, our results are truthful by using laser corrections. We could test, by getting spatial resolution on emission points localization in gaz chamber, the capacity of the acquisition system to select the interesting calibration events. We also noticed a slight dissymetry in vertex longitudinal reconstruction which indicates an anomaly in reconstruction formula. The NEMO3 detector is now operating since the setup of the full shield (iron and neutron shielding) and another calibration session must be performed during the summer 2002.


Table des matières


Liste des figures

  1. Diagramme de Kurie dans le cas où $ m_{\nu}=0$ (ligne solide) et $ m_{\nu}\neq 0$ (ligne pointillée)
  2. Processus de désintégration $ \beta\beta(2\nu)$
  3. Somme de l'énergie cinétique E des électrons sur $ E_{0}$ l'énergie disponible dans la réaction pour les 2 désintégrations $ \beta\beta(2\nu)$ et $ \beta\beta(0\nu)$
  4. Diagramme du processus $ \beta\beta(0\nu)$ dans le cas de courants gauches (a) ou dans le cas de deux vertex de chiralités différentes (b)
  5. Le détecteur NEMO3.
  6. Un des 20 secteurs de NEMO3.
  7. Schéma d'une cellule de dérive dit cellule Geiger.
  8. Photomultiplicateur Hamamatsu 5" RS6594
  9. Photomultiplicateur Hamamatsu 3" RS6091
  10. Schéma montrant la position des sources de calibration dans le détecteur NEMO3
  11. Schéma de désintégration du $ {}^{207}$Bi
  12. Carte des vertex reconstruits sur les feuilles sources des 20 secteurs en utilisant uniquement les compteurs internes
  13. Distribution de la position longitudinale et transversale des vertex reconstruits sur les compteurs externes et ajustement par la fonction suivante: $ P1+P2 . exp^{\big(-\frac{(X-P3)^2}{2 P4^2}\big)}$
  14. Spectre en énergie du $ {}^{207}$Bi dans le canal 1 électron pour l'ensemble des PM du calorimètre
  15. Spectre en énergie du $ {}^{207}$Bi dans le canal 1 électron pour 1 photomultiplicateur du mur externe
  16. Résultats de calibration $ {}^{207}$Bi pour 1 photomultiplicateur
  17. Exemple de fit sur la queue du spectre $ \beta$($ {}^{90}$Y)
  18. Schéma du système laser de calibration relative
  19. Comparaison entre la distribution non corrigée et corrigée de la pente de calibrage
  20. Distribution de l'offset obtenu à partir des runs de $ {}^{207}$Bi: en rouge le fit "forcé" (3 points) et en bleu le fit sur deux points
  21. Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ -5<\beta<5$keV
  22. Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ 5<\beta<15$keV
  23. Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ 15<\beta<25$keV
  24. Comparaison entre les deux paramètres de calibration $ {}^{90}$Y et $ {}^{207}$Bi: alpha est la pente de la droite de calibrage en keV/canal d'ADC

Introduction

Découvert par l'expérience il y a plus de 40 ans, le neutrino fait toujours l'objet de nombreuses recherches. En effet, sa nature demeure encore aujourd'hui pour la physique des particules une question ouverte. Son absence de charge et son caractère fermionique lui confèrent une situation particulière et permettent dans le cadre du Modèle Standard électrofaible et de ses extensions de le définir selon deux manières différentes: soit le neutrino est représenté par un champ de Dirac et alors le neutrino et l'antineutrino sont deux particules distinctes comme tous les autres fermions chargés mais avec la particularité d'avoir une masse nulle, soit le neutrino est représenté par un champ de Majorana et alors le neutrino et l'antineutrino sont une même particule massive. La nature Majorana du neutrino pourrait a priori s'imposer sachant qu'il n'y a pas d'autre nombre quantique additif pour cette particule. Cependant, les meilleures limites supérieures obtenues aujourd'hui sur sa masse effective sont de l'ordre de 1 eV; elles ne permettent donc pas d'affirmer avec certitude le caractère massif du neutrino.
L'expérience NEMO a pour but de mettre en évidence la double désintégration bêta sans émission de neutrinos. Cette décroissance permettrait de prouver en dessous d'une certaine sensibilité l'existence de neutrinos massifs de Majorana. Débuté en 1998, ce programme de recherche est maintenant dans sa phase finale avec l'achèvement de l'assemblage du détecteur NEMO3 prévu pour Juillet 2002.
L'objet de ce travail est le traitement de données issues des différentes séances de calibrage du calorimètre NEMO3 effectuées en Avril 2002. Après avoir présenté dans les deux premières parties la physique du neutrino et le détecteur NEMO3 en insistant notamment sur le calorimètre, je consacrerai la troisième partie à la description du dispositif expérimental utilisé, à l'analyse des événements de calibrage ainsi qu'aux résultats obtenus durant cette séance.

Physique du Neutrino

Historique

C'est en 1930 que Pauli fit l'hypothèse de l'existence d'une particule nouvelle, neutre, intéragissant très faiblement avec la matière et accompagnant l'émission de l'électron lors du processus de désintégration $ \beta$ pour expliquer la continuité du spectre en énergie des électrons.
Aujourd'hui, nous savons que le neutrino est une particule élémentaire de spin 1/2 et de charge électrique nulle. Le neutrino ne peut interagir que par interaction faible. Il y a 3 espèces ou saveurs de neutrinos: $ \nu_{e}$, $ \nu_{\mu}$, $ \nu_{\tau}$. Alors que les neutrinos $ \nu_{e}$ et $ \nu_{\mu}$ ont été découverts respectivement en 1953 et en 1962, ce n'est qu'en 2000 que l'expérience DONUT a mis en évidence pour la première fois 4 interactions du neutrino $ \nu_{\tau}$.
La détermination de la masse des neutrinos ($ \nu_{e}$, $ \nu_{\mu}$, $ \nu_{\tau}$) est l'un des thèmes majeurs de recherche dans la physique du neutrino. Nous ne disposons actuellement que de limites supérieures:

\begin{displaymath} \left \{ \begin{array}{cc} m_{\nu_{e}} < 2.8eV (95\%CL) & (... ...({\tau}^{-} \rightarrow 5\pi + \nu_{\tau}) \end{array}\right. \end{displaymath}

Dans l'hypothèse où le neutrino est massif, sa masse demeure très petite devant la masse des autres particules élémentaires, ce qui est l'un des principaux problèmes théoriques.

Le Neutrino dans le modèle Standard et ses extensions

Neutrino de Dirac

Le neutrino est décrit dans le cadre du modèle standard comme une particule de masse nulle, stable, et d'hélicité gauche (hélicité droite pour l'antineutrino). Le neutrino étant de spin 1/2, il peut être décrit par un bi-spineur $ \psi$ vérifiant l'équation de Dirac ($ \hbar=c=1$):

$\displaystyle (i\gamma_{\mu}\partial^{\mu}-m) \psi = 0$ (1.1)

avec $ m$ sa masse au repos et $ \gamma_{\mu}$ les matrices de Dirac. Cette équation admet 2 solutions correspondant à 4 cas physiques. La première solution représente le neutrino et s'écrit:

$\displaystyle \psi=\binom{\psi_{L}}{0}+\binom{0}{\psi_{R}}$ (1.2)

$ \psi_{L}$ et $ \psi_{R}$ sont deux composantes chirales gauche et droite qui sont image l'une de l'autre par parité (à une phase près). On note alors $ \nu_{L}$ et $ \nu_{R}$ les neutrinos de chiralité gauche et droite. La deuxième solution représente l'antineutrino suivant 2 composantes de chiralité gauche et droite: $ \bar\nu_{L}$ et $ \bar\nu_{R}$.
($ \nu_{L}$, $ \nu_{R}$, $ \bar\nu_{L}$, $ \bar\nu_{R}$) représentent donc 4 solutions indépendantes associées au neutrino de Dirac. Etant donné que le modèle standard décrit le neutrino comme une particule de masse nulle et d'hélicité gauche, il ne reste plus que 2 neutrinos (dit de Weyl) conformément à l'expérience: le neutrino $ \nu_{L}$ et l'antineutrino $ \bar\nu_{R}$.

Neutrino de Majorana

En 1937, Ettore Majorana émis l'hypothèse que le neutrino et l'antineutrino n'étaient qu'une seule et même particule. Il ne reste plus alors que 2 états possibles pour le neutrino: $ \nu_{+}$ et $ \nu_{-}$ qui correspondent respectivement à un état d'hélicité droite et gauche. On démontre alors que la particule de Majorana doit être massive pour qu'il puisse exister une transformation de Lorentz permettant le passage d'un état d'hélicité à un autre.
Si le neutrino est massif, il faut encore comprendre pourquoi sa masse est bien plus petite que celle des autres fermions. Le mécanisme de balançoire peut expliquer cet écart.

Le mécanisme de balançoire

Le but ici est de construire dans le cadre le plus général le terme de masse $ L_{m}$ du Lagrangien. On utilise pour cela 2 scalaires invariants de Lorentz: $ \bar\psi\psi$ et $ \bar\psi\psi^{C}$. Dans les extensions du modèle Standard, nous devons considérer les 2 termes de masse[1]:

-
un terme de masse de Dirac: $ m\bar\psi\psi$ = $ m_{D}(\bar\psi_{L}\psi_{R}+\bar\psi_{R}\psi_{L})$
-
un terme de masse de Majorana: $ m\bar\psi\psi^{C}$ = $ m(\bar\psi_{L}\psi_{R}^{C}+\bar\psi_{R}\psi_{L}^{C})$
Le terme de masse s'écrit alors en prenant en compte les deux champs précédents:

$\displaystyle -L_{m}=m_{D}\bar\psi_{L}\psi_{R}+\frac{1}{2}m_{L}\bar\psi_{L}\psi_{R}^{C}+\frac{1}{2}m_{R}\bar\psi_{R}\psi_{L}^{C}+hc$ (1.3)

où $ hc$ est l'hermitien conjugué, $ m_{D}$ est la masse de Dirac, $ m_{L}$ est la masse de Majorana gauche et $ m_{R}$ la masse de Majorana droite. Le Lagrangien peut alors se mettre sous la forme:

$ -L_{m}=\frac{1}{2}(\bar\chi,\bar\omega)$$\displaystyle \begin{pmatrix}m_{L} & m_{D} \ m_{D} & m_{R} \end{pmatrix} \begin{pmatrix}\chi \ \omega \end{pmatrix}$ (1.4)

où $ \chi=\psi_{L}+\psi_{R}^{C}$ et $ \omega=\psi_{R}+\psi_{L}^{C}$. Il apparaît ici la matrice de masse M dont la dimension est fixée par le nombre de neutrinos gauches ($ n_{L}=3$) et droits ($ n_{R}$):

   M=$\displaystyle \begin{pmatrix} m_{L} & m_{D} \\ m_{D} & m_{R} \end{pmatrix}$

Cette matrice est diagonalisable à l'aide d'une matrice unitaire $ U$. On obtient alors les états de saveurs $ \nu_{l}$ ($ l$=$ e$, $ \nu$ et $ \tau$) en fonction des états propres de masse $ \nu_{i}$ ($ i$=1,..,3+$ n_{R}$) par la relation:

$\displaystyle \nu_{l}=\sum_{i=1}^{3+n_{R}}U_{li}\nu_{i}$ (1.5)

Dans le cas d'une seule génération de neutrinos, on obtient les 2 valeurs propres de masse suivantes:

$\displaystyle m_{1,2}=\frac{1}{2}(m_{L}+m_{R}\pm \sqrt{(m_{L}-m_{R})^2+4m_{D}^2})$ (1.6)

On peut envisager à partir de cette expression 3 cas:

-
$ m_{L}=m_{R}=0$: les neutrinos sont de purs neutrinos de Dirac de masse $ m_{D}$ pour chacune des composantes gauche et droite.
-
$ m_{D}=0$: les neutrinos sont de pures particules de Majorana de masse $ m_{L}$ pour la composante gauche et de $ m_{R}$ pour la composante droite.
-
$ m_{L}\neq m_{R}\neq m_{D} $: on distingue alors 2 cas :
-si $ m_{D}\gg m_{R}$ et $ m_{D}\gg m_{L}$, les neutrinos sont qualifiés de neutrinos pseudo-Dirac.
-aucune expérience jusqu'à présent n'a mis en évidence l'interaction du neutrino droit, ce qui peut supposer que la valeur propre de masse $ m_{R}$ est très grande devant $ m_{L}$ et $ m_{D}$. Les 2 solutions font apparaître par un développement limité au premier ordre un couple constitué d'un neutrino léger ($ m_{1}$) et d'un neutrino lourd ($ m_{2}$):

\begin{displaymath} \left \{ \begin{array}{cc} m_{1} &=\frac{m_{D}^2}{m_{R}}\ll m_{D} \\ m_{2} &=m_{R} \end{array}\right. \end{displaymath}

$ m_{D}$ étant de l'ordre de grandeur de la masse des fermions, ce mécanisme appelé aussi "see saw"[2] justifie la masse naturellement faible des neutrinos (ici $ m_{1})$ par rapport aux autres particules tout en conservant la hiérarchie $ m_{\nu_{e}}\ll m_{\nu_{\mu}}\ll m_{\nu_{\tau}}$.
Notons que les expériences à haute énergie ne peuvent conclure sur la nature du neutrino car à ces énergies, les états de saveurs et les états propres de masse se confondent. Nous verrons comment le processus de décroissance $ \beta\beta(0\nu)$, à des énergies de l'ordre du MeV, peut nous conduire à mieux étudier la nature du neutrino.

Recherche de la masse des neutrinos

De nombreuses expériences cherchent à déterminer la masse des neutrinos. Nous en présentons ici deux avant de parler plus précisemment de la double désintégration $ \beta$ dans la section suivante. La première est historiquement la désintégration $ \beta$. L'étude de la cinématique de la réaction $ \beta$ permet de fixer une limite supérieure sur la masse du neutrino. En effet, le spectre d'énergie de la décroissance $ \beta$ est proportionnel à:

$\displaystyle N(p_{e})\propto p_{e}^{2}F(Z,E_{e})(E_{0}-E_{e})^{2}\sqrt{1-\left(\frac{m_{\nu_{e}}c^{2}}{E_{0}-E_{e}}\right)^{2}}$ (1.7)

avec $ p_{e}$ la quantité de mouvement de l'électron, $ F(Z,E_{e})$ la fonction de Fermi, $ E_{0}$ l'énergie disponible, $ E_{e}$ l'énergie cinétique de l'électron et $ m_{\nu_{e}}$ la masse du neutrino $ \nu_{e}$. On représente habituellement la quantité $ \sqrt{\frac{N(p_{e})}{p_{e}^{2}F}}$ en fonction de $ E_{e}$: c'est la droite de Kurie qui est représentée sur la figure1.1.

Figure 1.1: Diagramme de Kurie dans le cas où $ m_{\nu}=0$ (ligne solide) et $ m_{\nu}\neq 0$ (ligne pointillée)
\includegraphics[width=10cm height=7cm]{kurie.eps}

Si $ m_{\nu_{e}} =0$, cette droite coupe l'axe des abcisses en $ E_{e}=E_{0}$. Si $ m_{\nu_{e}} \neq 0$, elle le coupe à une énergie $ E_{e}$ inférieure à la précédente ( $ E_{0}-m_{\nu_{e}}c^{2}$). On peut ainsi déterminer une limite supérieure sur la masse du neutrino. Les résultats obtenus sur le tritium donnent: $ m_{\nu_{e}}< 2.8eV$[3].

La deuxième expérience est la recherche d'oscillations de neutrinos. En effet, en partant de l'équation (1.5) qui donne la relation entre les états propres de masse et les états de saveurs au moyen d'une matrice unitaire $ U$, nous considérons le cas simple de mélange entre deux états de masse $ \nu_{1}$ et $ \nu_{2}$. La matrice $ U$ peut alors s'écrire:

$ U=$$\displaystyle \begin{pmatrix}\cos \theta & \sin \theta \ -\sin \theta & \cos \theta \end{pmatrix}$ (1.8)

où $ \theta$ est l'angle de mélange en analogie avec la matrice de rotation. Si l'on prend deux saveurs de neutrinos quelconques $ \alpha$ et $ \beta$, la probabilité pour qu'à l'instant t, le neutrino $ \alpha$ se comporte comme un neutrino $ \beta$ est donnée par:

$\displaystyle P(\nu_{\alpha} \rightarrow \nu_{\beta},t)=\sin^{2}2\theta \sin^{2} \frac{\Delta m^{2}t}{4E}$ (1.9)

Cette relation fait apparaître une amplitude $ \sin^{2}\theta$ qui oscille avec une période $ T=\pi \frac{4E}{\Delta m^{2}}$ et avec une longueur d'oscillation $ L_{osc}=cT$. Ce phénomène est donc observable à condition que les états propres de l'interaction faible soient différents des états propres de masse.

Recherche de la masse du neutrino par
la décroissance double bêta

La désintégration double bêta avec émission de deux neutrinos ( $ \beta\beta(2\nu)$) fut prédite en 1935 par Goeppert-Mayer [4]mais ce n'est qu'en 1968 qu'elle fut mise en évidence expérimentalement. Elle correspond à la transformation spontanée de 2 neutrons en 2 protons avec l'émission de 2 électrons et de 2 antineutrinos: elle peut être décrite comme deux émissions $ \beta$ simultanées (Fig1.2). La décroissance $ \beta\beta^{+}$ existe aussi mais sa probabilité de transition est faible devant celle des émetteurs $ \beta\beta^{-}$.

Figure 1.2: Processus de désintégration $ \beta\beta(2\nu)$

Un noyau $ _{Z}^{A}$X émetteur $ \beta\beta(2\nu)^{-}$ donne:

$\displaystyle (A,Z) \rightarrow (A,Z+2) + 2e^{-} + 2\bar\nu_{e}$    

Furry proposa en 1939 la double désintégration $ \beta$ sans émission de neutrinos. Ce processus est interdit par le modèle standard car il n'y a pas conservation du nombre leptonique:

$\displaystyle (A,Z) \rightarrow (A,Z+2) + 2e^{-}$    

Ces 2 processus sont extrêmement rares. La demi-vie de la désintégration $ \beta\beta(2\nu)$ donne une valeur allant environ de 10$ ^{19}$ années ($ ^{100}$Mo,$ ^{116}$Cd,$ ^{96}$Zn) à 10$ ^{24}$ années ($ ^{128}$Te). Le spectre de l'énergie cinétique des 2 électrons émis pour la désintégration $ \beta\beta(2\nu)$ est continu car une partie de l'énergie disponible est emportée par les 2 neutrinos. Par contre, le spectre pour la $ \beta\beta(0\nu)$ est théoriquement une raie (en négligeant l'énergie de recul du noyau) dont l'énergie est égale à l'énergie $ Q_{\beta\beta}$ de la réaction. La figure ci-dessous(Fig1.3) montre pour les 2 processus le spectre attendu.

Figure 1.3: Somme de l'énergie cinétique E des électrons sur $ E_{0}$ l'énergie disponible dans la réaction pour les 2 désintégrations $ \beta\beta(2\nu)$ et $ \beta\beta(0\nu)$
\includegraphics[width=10cm height=7cm]{spectrebb.eps}

La résolution finie des détecteurs fait que la désintégration $ \beta\beta(0\nu)$ possède une certaine largeur. La désintégration $ \beta\beta(2\nu)$ est donc un bruit de fond permanent pour l'étude du processus $ \beta\beta(0\nu)$ interdit, d'où la nécessité d'étudier le processus $ \beta\beta(2\nu)$ permis.
La double désintégration $ \beta$ n'est possible que si la masse du noyau père $ _{Z}^{A}$X est plus grande que la masse du noyau fils $ _{Z+2}^{\hspace{4mm}A}$X et si la désintégration $ \beta$ est énergétiquement interdite ( $ M(A,Z+1) > M(A,Z)$). On démontre que les seuls noyaux produisant une radioactivité $ \beta\beta$ sont des noyaux pair-pair. Lors d'une désintégration $ \beta\beta$, les transitions sont en majorité des transitions 0$ ^{+}$ $ \rightarrow$ 0$ ^{+}$ mais il est énergétiquement possible d'observer une transition 0$ ^{+}$ du père vers des niveaux excités 0$ ^{+}$ ou 2$ ^{+}$ du noyau fils.

demi-vie de la désintégration $ \beta\beta(2\nu)$

Dans le cas de la désintégration $ \beta\beta(2\nu)$ permise, la demi-vie du processus s'écrit:

$\displaystyle \big(T_{1/2}^{2\nu}\big)^{-1}=C_{2\nu} \Bigg[ M_{GT}^{2\nu}-\bigg(\frac{g_{V}}{g_{A}} \bigg)^2 M_{F}^{2\nu} \Bigg]^2$ (1.10)

avec:

-
$ C_{2\nu}$ est le terme d'espace de phase tenant compte des effets Coulombiens; il dépend de l'énergie disponible $ Q_{\beta\beta}$.
-
$ M_{GT}^{2\nu}$ et $ M_{F}^{2\nu}$ sont les éléments de matrice nucléaire de Gamow-Teller et de Fermi ($ g_{V}$ et $ g_{A}$ sont des constantes de couplage vectorielle et axiale).

L'estimation de cette demi-vie est très difficile: pour un même noyau, les éléments de matrice nucléaire peuvent varier selon les auteurs d'un facteur 3. Elle permet néanmoins de valider la méthode de calcul employée pour le calcul des éléments de matrice du processus $ \beta\beta(0\nu)$.

Le tableau 1.1 rassemble tous les émetteurs $ \beta\beta$ ayant un $ Q_{\beta\beta}$ supérieur à 2.615 MeV (raie $ \gamma$ du $ {}^{208}$Tl) qui correspond à la raie la plus énergétique dans la radioactivité naturelle. Nous verrons dans le prochain chapitre comment l'expérience NEMO3 tire profit de ces noyaux.


Tableau 1.1: Noyaux candidats pour la désintégration $ \beta^{-}\beta^{-}$
Transition $ Q_{\beta\beta}$ (keV) Abondance (%)
$ {}^{116}$Cd $ \rightarrow$ $ {}^{116}$Sn 2802 $ \pm$ 4 7
$ {}^{82}$Se $ \rightarrow$ $ {}^{82}$Kr 2995 $ \pm$ 6 9
$ {}^{100}$Mo $ \rightarrow$ $ {}^{100}$Ru 3034 $ \pm$ 6 10
$ {}^{96}$Zr $ \rightarrow$ $ {}^{96}$Mo 3350 $ \pm$ 3 3
$ {}^{150}$Nd $ \rightarrow$ $ {}^{150}$Sm 3667 $ \pm$ 2 6
$ {}^{48}$Ca $ \rightarrow$ $ {}^{48}$Ti 4271 $ \pm$ 4 0.2


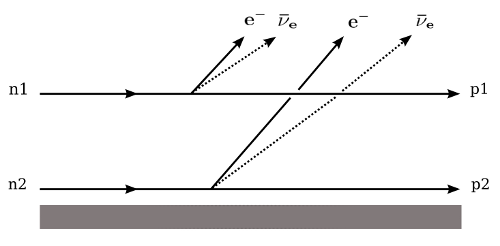
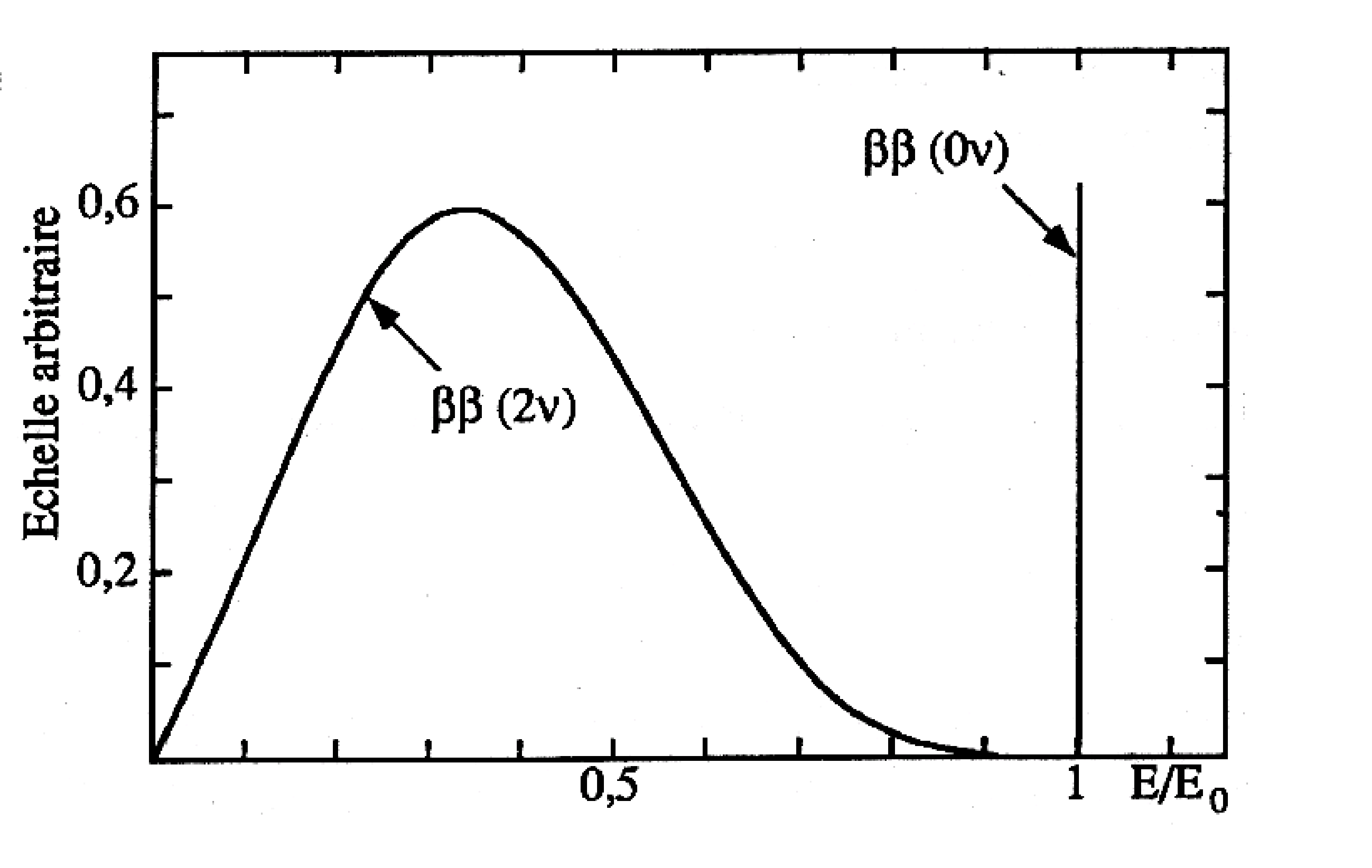
demi-vie de la désintégration $ \beta\beta(0\nu)$

La période du processus $ \beta\beta(0\nu)$ peut s'écrire :

$\displaystyle \big(T_{1/2}^{0\nu}\big)^{-1}=C_{0\nu} \Bigg[ M_{GT}^{0\nu}-\bigg(\frac{g_{V}}{g_{A}} \bigg)^2 M_{F}^{0\nu} \Bigg]^2 \langle m_{\nu} \rangle^{2}$ (1.11)

Les éléments de matrice nucléaire des transitions de Gamov-Teller et de Fermi sont très différents des éléments de matrice du processus $ \beta\beta(2\nu)$ car le propagateur du neutrino intervient. Le terme $ \langle m_{\nu} \rangle$, qui représente la masse effective du neutrino, est obtenu à partir de ce même propagateur et s'exprime en fonction des états propres de masse par une relation déduite de l'équation (1.5):

$\displaystyle \langle m_{\nu_{e}} \rangle=\bigg\vert\sum_{i}U_{ei}^{2} m_{i}\bigg\vert$ (1.12)

On peut donc en déduire la valeur de la masse effective en ayant déterminé auparavant les éléments de matrice nucléaire. Cette décroissance a lieu si l'antineutrino d'hélicité droite émis au premier vertex est absorbé au second vertex comme un neutrino d'hélicité gauche. Ceci implique que, si l'interaction faible est purement V-A (Fig1.4a), alors le neutrino et l'antineutrino sont une même particule et l'observation du changement d'hélicité rend cette particule massive. Par contre, si les courants ne sont plus purement V-A (avec une composante V+A), il n'est plus nécessaire d'observer un changement d'hélicité pour pouvoir justifier la masse non nulle de cette particule(Fig1.4b). Ces courants V+A pourraient être mis en évidence dans le cas où l'on observerait des événements $ \beta\beta(0\nu)$ entre les niveaux 0$ ^{+}$ du père et 2$ ^{+}$ du fils. Dans tous les cas, l'observation du processus $ \beta\beta(0\nu)$ prouverait l'existence d'un neutrino massif de Majorana.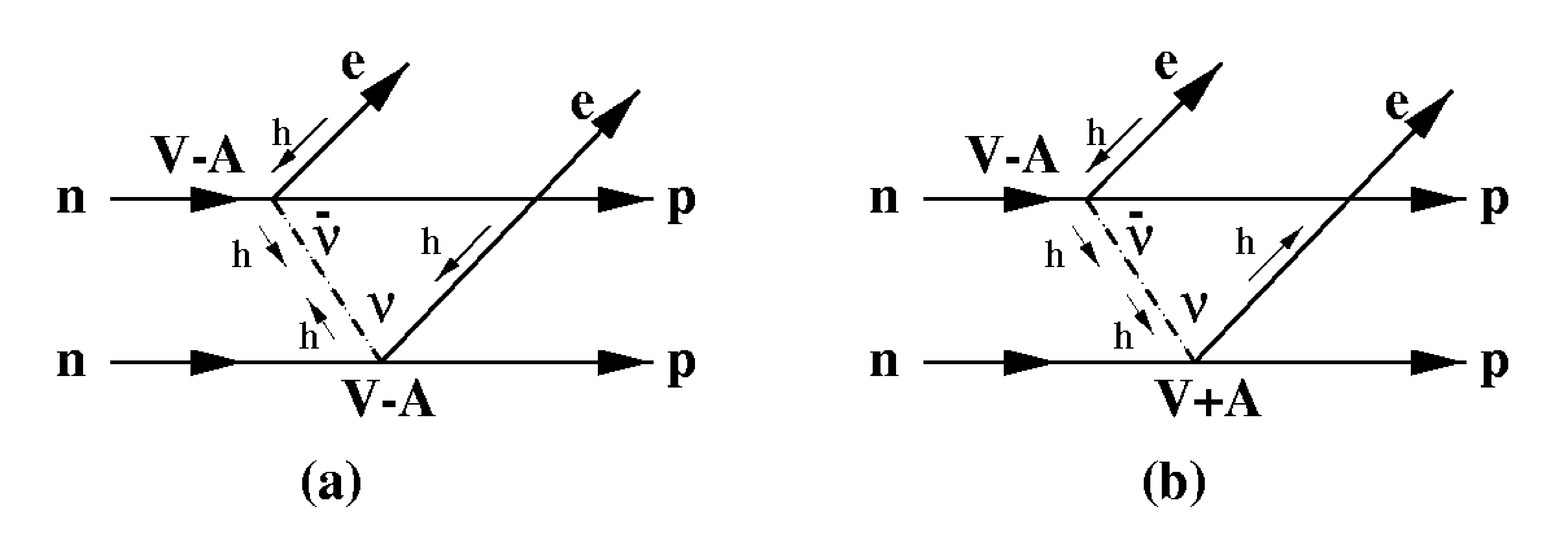

Figure 1.4: Diagramme du processus $ \beta\beta(0\nu)$ dans le cas de courants gauches (a) ou dans le cas de deux vertex de chiralités différentes (b)
\includegraphics[width=10cm height=4cm]{proc2.eps}

Expériences sur la désintégration $ \beta\beta$

Les expériences qui distinguent la $ \beta\beta(2\nu)$ et la $ \beta\beta(0\nu)$ sont de deux types:

-
source=détecteur: ce type d'expérience présente l'avantage d'avoir une efficacité proche de 100% car la source est utilisée comme détecteur. Cependant, l'étude du bruit de fond est limitée par le fait que le détecteur n'est sensible qu'au spectre d'énergie des 2 électrons: on distingue alors simplement la raie $ \beta\beta(0\nu)$ du spectre continu $ \beta\beta(2\nu)$. Une des expériences de ce type les plus connues est celle de la collaboration Heidelberg-Moscou[5] qui utilise un émetteur double $ \beta\beta$ possédant une excellente résolution en énergie: le $ ^{76}$Ge.

-
source$ \neq$détecteur: le principal avantage de ces expériences, comme celle de NEMO3, est de pouvoir étudier plusieurs noyaux. De plus, la réjection du bruit de fond est facilitée par la reconstruction de la trajectoire des 2 électrons. Ces expériences sont toutefois limitées par la quantité d'isotope à utiliser car les pertes d'énergie des électrons ne doivent pas être trop grandes. Nous pouvons citer, en plus de NEMO3 qui utilise un détecteur de traces gazeux, l'expérience TGV qui utilise des détecteurs à base de germanium entre lesquels sont placées de minces feuilles d'émetteurs double bêta.

Sensibilité d'une expérience $ \beta\beta$ au processus $ \beta\beta(0\nu)$

Prenons le cas où l'on dispose d'une masse M d'isotope avec laquelle nous observons $ N_{s}$ événements $ \beta\beta(0\nu)$ pendant une durée $ \Delta t$ avec une efficacité $ \epsilon$; la demi-vie s'écrit alors:

$\displaystyle T_{1/2}^{0\nu}=\frac{\ln2 N_{A}}{A} \bigg[ \frac{M \epsilon \Delta t}{N_{s}} \bigg]$ (1.13)

avec $ A$ la masse atomique de l'isotope et $ N_{A}$ le nombre d'Avogadro. Nous pouvons minorer cette période en prenant le cas où il n'y a aucun événement de bruit de fond (estimé par simulation) ni d'événements observés dans la région où l'on attend le signal. En prenant le nombre d'événements $ \beta\beta(0\nu)$ exclus égal à $ N_{ex}$=2,3 (90% de niveau de confiance), nous pouvons écrire:

$\displaystyle T_{1/2}^{0\nu}>\bigg(T_{1/2}^{0\nu}\bigg)_{lim}=\frac{\ln2 N_{A}}{A} \bigg[ \frac{M \epsilon \Delta t}{N_{ex}} \bigg]$ (1.14)

d'où l'on déduit une limite supérieure sur la masse effective du neutrino:

$\displaystyle \langle m_{\nu}\rangle < \langle m_{\nu}\rangle_{lim}=\sqrt{\fr... ...t{C_{0\nu}}\vert M^{0\nu}\vert} \sqrt{\frac{1}{M \Delta t \epsilon}} $(90% CL) (1.15)




Pour multiplier les chances d'observer le processus $ \beta\beta(0\nu)$, la collaboration NEMO a choisi des sources en fonction des critères donnés par l'inégalité précédente:

-
il faut que M soit la plus grande possible, ce qui revient à privilégier des émetteurs dont l'abondance isotopique est grande.
-
Le facteur $ \frac{1}{\sqrt{C_{0\nu}}\vert M^{0\nu}\vert}$ doit être le plus faible possible. Les théoriciens s'accordent à dire que le Molybdène 100 et le Néodyme 150 font parti des noyaux qui satisfont le mieux cette condition.
-
il faut que $ N_{ex}$ soit le plus faible possible, c'est à dire que le bruit de fond soit réduit au maximum en utilisant des émétteurs dont le $ Q_{\beta\beta}$ est supérieur à la radioactivité naturelle.

Dans l'expérience NEMO3, c'est le Molybdène 100 qui est principalement utilisé car, en plus d'offrir un bon compromis sur les deux derniers critères, nous pouvons contrairement à des émetteurs dont l'abondance est faible, en disposer d'une quantité satisfaisante pour l'expérience (10 kg). Un autre émetteur $ \beta\beta$ utilisé est le $ ^{82}$Se: il présente l'avantage d'avoir une période $ T_{1/2}^{2\nu}$ plus élevée que le molybdène 100 et donc un bruit de fond dû au signal $ \beta\beta(2\nu)$ plus faible.

L'intérêt de l'expérience NEMO est la précision avec laquelle va être déterminée la masse effective du neutrino. Le tableau 1.2[1] résume les limites sur $ T_{1/2}^{0\nu}$ et sur $ \langle m_{\nu} \rangle$ que l'on obtient à 90 % de niveau de confiance sur 5 ans de données avec les 2 principales sources utilisées ($ ^{100}$Mo et $ ^{82}$Se).


Tableau 1.2: Nombre d'événements de bruit de fond et sensibilité attendue (90%CL) dans la fenêtre [2.8;3.2]MeV après 5 ans de prises de données avec 7 kg de $ ^{100}$Mo et 1 kg de $ ^{82}$Se.
Isotope $ ^{100}$Mo $ ^{82}$Se
  6 evts de bruit de fond attendu 2 evts de bruit de fond attendu
  6 evts observés 2 evts observés
  5 evts $ \beta\beta(0\nu)$ exclus 4 evts $ \beta\beta(0\nu)$ exclus
$ T_{1/2}^{0\nu}$ $ >$ 3.7 10$ ^{24}$ ans $ >$ 7.9 10$ ^{23}$ ans
$ \langle m_{\nu} \rangle$ $ <$ 0.25 - 0.7 eV $ <$ 0.8 - 1.6 eV


Description de l'expérience
NEMO3

Nous allons maintenant présenter l'expérience NEMO3 en insistant notamment sur le fonctionnement du calorimètre. Ceci nous permettra de mieux comprendre la méthode de calibration développée au chapitre 3.

Le laboratoire Souterrain de Modane (LSM)

L'ensemble du détecteur se trouve dans le Laboratoire Souterrain de Modane situé dans le tunnel de Fréjus sous 1780 mètres de roche. Ce site a été retenu pour son faible bruit de fond naturel. En effet, à cette profondeur, le flux de muons cosmiques (4.2 muons/m$ ^{2}$/jour) est réduit d'un facteur 3.10$ ^{6}$ par rapport au niveau de la mer; celui des neutrons, venant principalement de la roche, est réduit d'un facteur 10$ ^{5}$ par rapport au sol et celui des rayonnements gamma (entre 3 et 32 MeV) d'un facteur 10$ ^{3}$. Tous ces éléments font de Modane l'un des laboratoires souterrains les mieux protégés au monde. Il est cependant nécessaire comme dans tout site souterrain d'avoir une ventilation suffisante pour limiter la présence de radon issu de la roche. Le Laboratoire est donc équipé d'un système de ventilation très performant relié à celui du tunnel de Fréjus.
Le LSM acceuille d'autres expériences nécessitant un environnement de basse radioactivité: l'expérience EDELWEISS qui recherche la matière noire par une méthode bolométrique ainsi que l'expérience TGV dont nous avons parlé dans le chapitre précédent.

Le détecteur NEMO3

Description générale

Le détecteur NEMO3 est un détecteur cylindrique (Fig2.1) d'environ 4 mètres de hauteur et 6 mètres de diamètre, scindé en 20 secteurs (Fig2.2). La chambre à fils réunit au total 6180 cellules Geiger: elles permettent la reconstruction des traces. Tout autour, 1940 scintillateurs couplés à des photomultiplicateurs, assurent les mesures en temps de vol et en énergie des particules.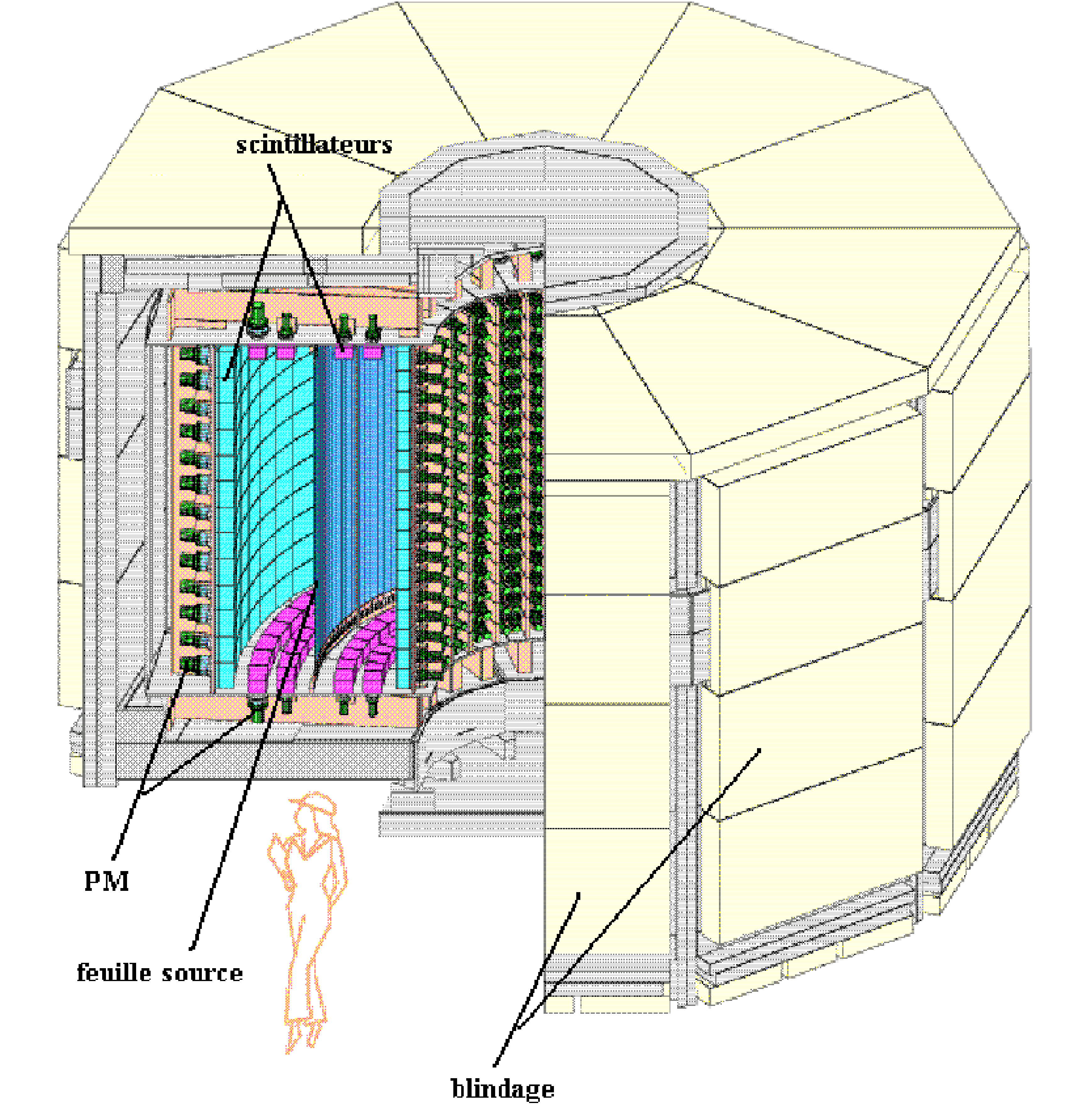

Figure 2.1: Le détecteur NEMO3.
\includegraphics[width=9cm height=9cm]{nemo-last.eps}

La géométrie cylindrique a été retenue afin d'augmenter l'efficacité du détecteur. La structure par secteur permet, quant à elle, de diviser le détecteur en 20 parties indépendantes. Il est par exemple possible de modifier la source émettrice double bêta d'un seul secteur pour utiliser différents isotopes.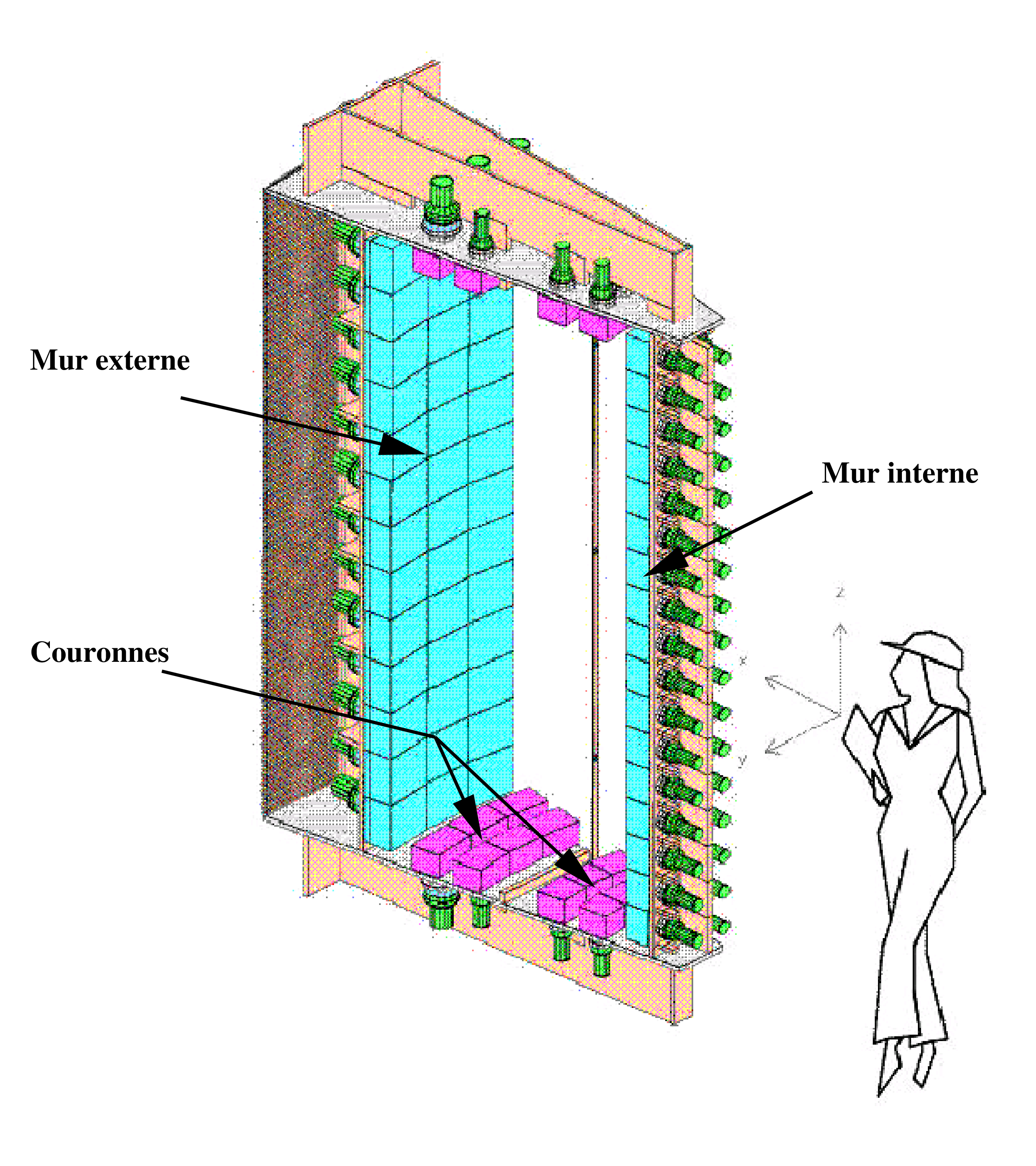
Afin de réduire le bruit de fond, un blindage de 20 cm de fer est installé autour du détecteur. Un blindage aux neutrons a été mis en place sur le contour du détecteur ainsi qu'une bobine magnétique permettant de différencier les paires (e$ ^+$,e$ ^-$) provenant du bruit de fond des événements (e$ ^-$,e$ ^-$) provenant de la décroissance double bêta.
L'ensemble du détecteur est placé sur une structure métallique d'environ 2 m de hauteur pour disposer de place pour loger l'électronique. Une tour située à l'intérieur du blindage donne accès aux murs de scintillateurs internes.

Figure 2.2: Un des 20 secteurs de NEMO3.
\includegraphics[width=8cm height=9cm]{secteur3.eps}

Détection du processus $ \beta\beta(0\nu)$

Dans ce dispositif, l'identification des événements $ \beta\beta(0\nu)$ repose sur l'observation de l'émission simultanée de deux électrons créant 2 traces issues du même vertex, et dont la somme des énergies mesurées par le calorimètre doit être égale à $ Q_{\beta\beta}$. La principale difficulté est alors de distinguer les événements $ \beta\beta$ des événements de bruit de fond dont les différentes origines sont expliquées dans le paragraphe suivant.

Sources de bruit de fond

Les origines du bruit de fond sont classées selon qu'elles soient internes ou externes à la source émettrice double bêta:

Bruit de fond d'origine interne

Les sources utilisées sont naturellement contaminées en $ ^{208}$Tl et en $ ^{214}$Bi (descendants respectifs de la chaîne du $ ^{232}$Th et de l'$ ^{238}$U). Ces deux émetteurs $ \beta$ peuvent simuler des événements $ \beta\beta$:

-
l'émission $ \beta$ peut être suivie par l'émission d'un électron de conversion.
-
le rayonnement $ \beta$ peut éjecter un second électron par diffusion de Möller.
-
les rayonnements $ \gamma$ de désexcitation peuvent accompagner la désintégration $ \beta$ en interagissant avec elle en créant un deuxième électron par diffusion Compton ou effet photoélectrique.

Il ne peut être éliminé que par des méthodes de purification qui existent sous deux formes: la première, dite physique, permet de faire migrer les impuretés à la surface du cristal. La deuxième, dite chimique, élimine les impuretés par précipité.
L'autre source de bruit interne est le processus $ \beta\beta(2\nu)$ car le signal $ \beta\beta(0\nu)$ est attendu à la fin de son spectre. Une des façons de le minimiser est de choisir une source dont la demi-vie $ T^{1/2}_{\beta\beta(2\nu)}$ est grande, ce qui est le cas pour le $ ^{100}$Mo: ( $ T^{1/2}_{\beta\beta(2\nu)}=0.95\pm0.4\pm0.09 10^{19}$ ans).

Bruit de fond d'origine externe

La radioactivité des matériaux composant le détecteur constitue la source prépondérante du bruit de fond externe (ex: $ {}^{214}$Bi et $ {}^{208}$Tl du verre des PM). La création d'événements à deux électrons simulant le processus $ \beta\beta(0\nu)$ peut aussi être due à une contamination située à proximité de la source.
L'autre source de contamination provient des deux gaz rares issus des chaînes d'Uranium et de Thorium: le Radon et le Thoron. Naturellement produit par les roches, le Radon peut facilement diffuser et pénétrer dans le détecteur. Un contrôle quotidien du taux de Radon ainsi qu'une bonne isolation du détecteur permettent de limiter cette contamination.
Des photons de haute énergie (supérieur à 3 MeV) créés par capture radiative des neutrons peuvent aussi constituer un bruit de fond. Pour limiter ce phénomène, un blindage constitué de 27 cm de bois dans les parties hautes et basses et de 30 cm d'eau tout autour du détecteur est en train d'être mis en place.

La source

La source est placée au centre du détecteur de traces. Elle est constituée de 140 bandes juxtaposées (7 par secteur) d'environ 2 m de hauteur, 7 cm de largeur et 60 $ \mu$m d'épaisseur. Cette géométrie permet d'introduire jusqu'à 10 kg de Molybdène 100. Les bandes sont fixées, en haut et en bas, sur de petits supports en cuivre. Entre chaque secteur, un tube en cuivre est prévu pour positionner les sources radioactives utiles à l'étalonnage en temps et en énergie. Grâce à la segmentation du détecteur, la collaboration projette, durant les premiers temps d'acquisition, d'utiliser simultanément les différents isotopes.

Le détecteur de traces

Description

6180 cellules Geiger, placées de part et d'autre de la source dans un mélange d'hélium et d'alcool(6%), permettent la reconstruction des trajectoires des particules chargées. Chaque cellule, d'environ 2,7 mètres de hauteur et 30 mm de diamètre, est constituée de 9 fils en inox de 50 $ \mu$m de diamètre dont un fil anodique central et 8 fils cathodiques périphériques (Fig2.3). Le diamètre des fils a été diminué de moitié par rapport au prototype précédent NEMO2, afin de minimiser les pertes d'énergie des électrons lors de leur traversée de la chambre à fils.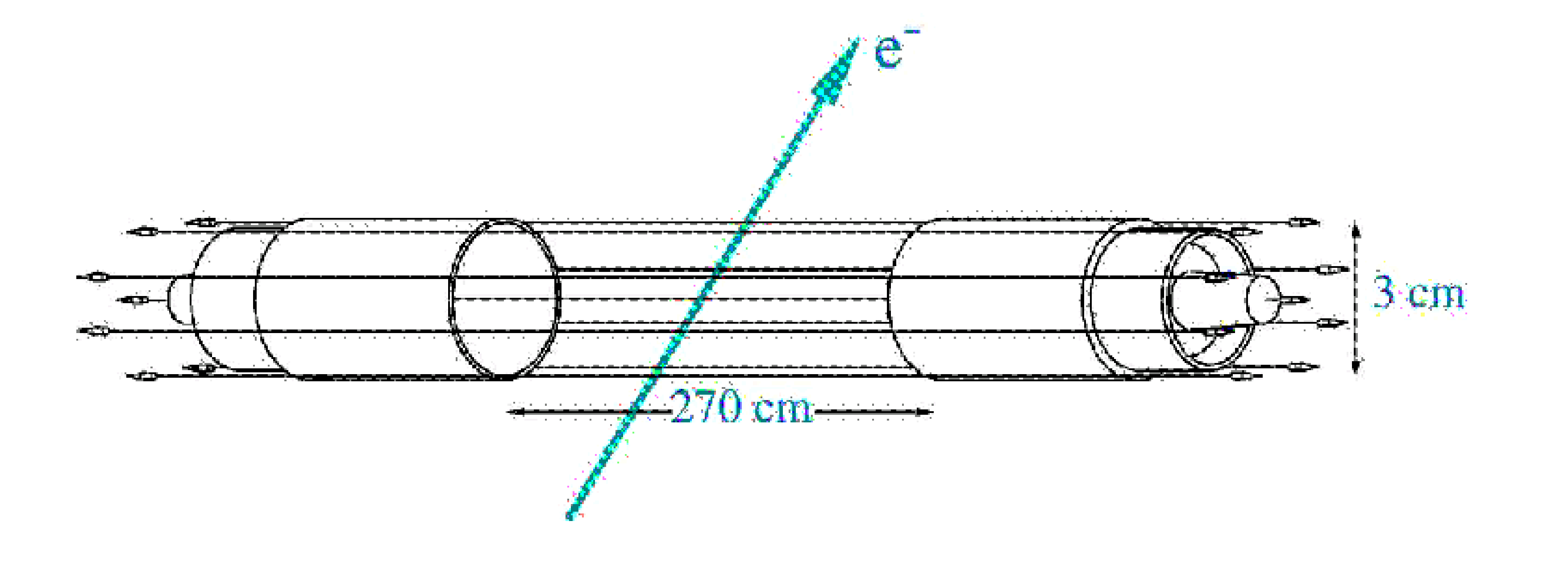
Toutes les cellules sont placées verticalement, le prototype NEMO2 ayant montré que l'alternance de plans de cellules verticales et horizontales était inutile et le temps de propagation du plasma suffisait à localiser avec précision la coordonnée longitudinale de la particule. Ces cellules sont disposées en rangées cylindriques: 9 de part et d'autre de la source double bêta. Par demi-chambre à fils, ces 9 rangées sont regroupées en 3 ensembles espacés d'une quinzaine de centimètres: un premier ensemble de 4 rangées près de la source, un deuxième ensemble de 2 rangées au milieu de la demi-chambre à fils et enfin un dernier ensemble de 3 rangées près des calorimètres.

Figure 2.3: Schéma d'une cellule de dérive dit cellule Geiger.
\includegraphics[width=10cm height=5cm]{geiger.eps}

Cette configuration "4-2-3" permet de localiser avec précision le vertex grâce aux quatre premières rangées, de déterminer le rayon de courbure (dans le cas d'un champ magnétique) ainsi que le scintillateur déclenché grâce aux autres rangées.

Performance du détecteur de traces

Le choix de la configuration 4-2-3 a été établi à partir de tests simulés portant sur la résolution des coordonnées de la trace en fonction de l'énergie de la particule et dans le cas d'un champ magnétique de 30 Gauss [6]. Lors du fonctionnement de la cellule, trois signaux sont enregistrés:

-
le signal anodique, produit par les électrons primaires et recolté à une extrémité du fil en bas d'un secteur
-
les deux signaux cathodiques obtenus lorsque le plasma Geiger atteind les deux extrémités.

Il est donc possible à partir de ces 3 signaux de reconstruire en 3 dimensions la trace des électrons; La résolution longitudinale est de l'ordre de 8mm et celle sur la position transverse de l'ordre de 500$ \mu$m. [6].

Le calorimètre

Description

Le calorimètre est formé de 1940 scintillateurs plastiques (97 par secteurs), couplés à des photomultiplicateurs. Ils sont répartis sur toute la surface du détecteur afin d'optimiser l'efficacité de détection des événements $ \beta\beta$(0$ \nu$). Les scintillateurs utilisés sont des scintillateurs plastiques produits par des membres de la collaboration. Sur les cotés, les scintillateurs, directement placés dans le mélange d'hélium et d'alcool, referment le détecteur de traces en formant deux murs cylindriques: un mur interne (rayon=90 cm) et un mur externe (rayon=220 cm). Ces murs sont constitués respectivement par secteur, de 2 rangées de 17 scintillateurs et de 3 rangées de 13 scintillateurs (Fig2.2). Le haut et le bas du détecteur, appelés "pétales" ou "couronnes", sont fermés par des plaques de fer sur lesquelles sont fixées 4 rangées de 3 scintillateurs, séparés par les rangées de cellules Geiger.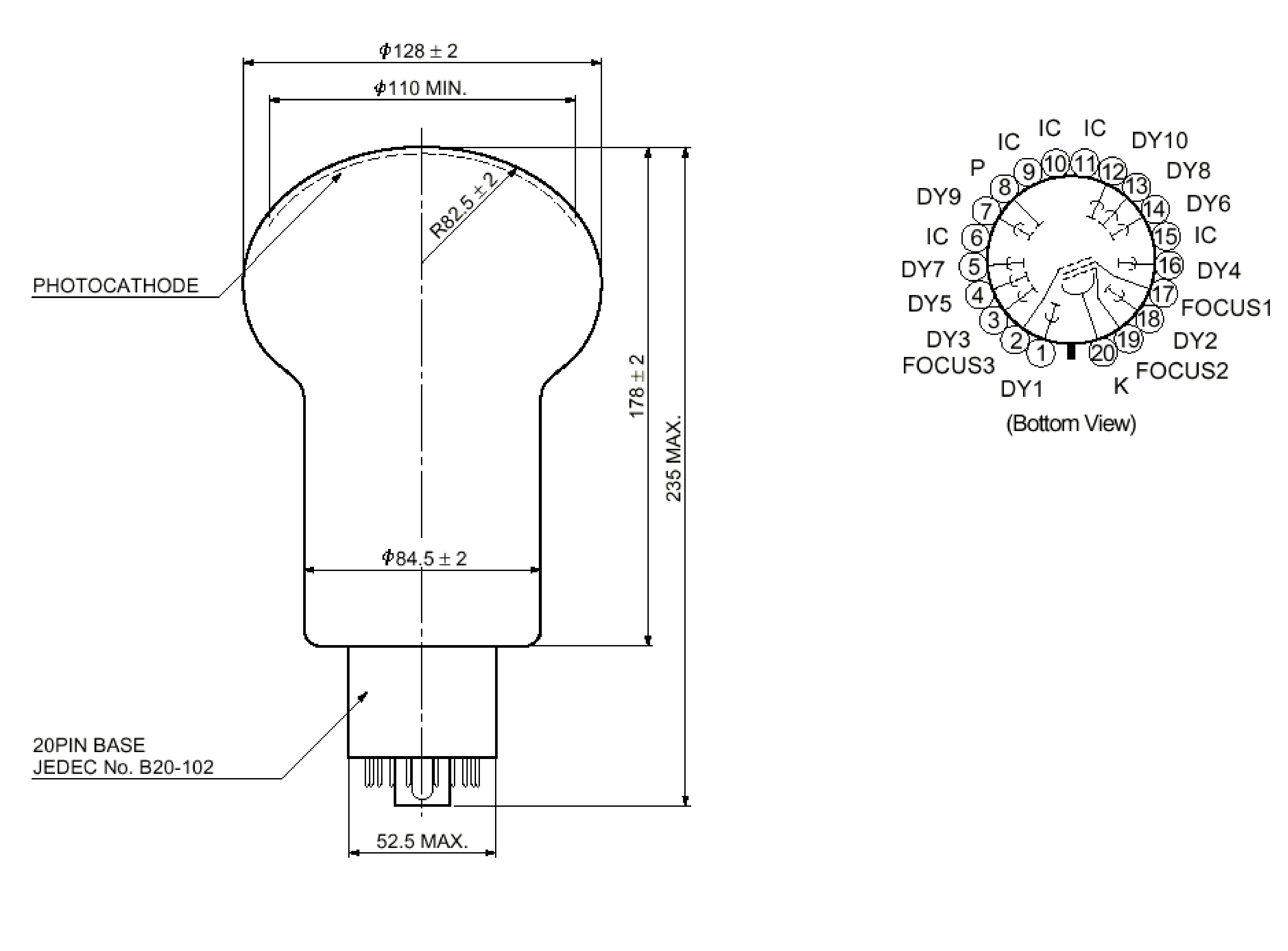

Figure 2.4: Photomultiplicateur Hamamatsu 5" RS6594
\includegraphics[width=7cm height=6cm]{hama5.eps}

Les scintillateurs de plus grande dimension, situés sur le mur externe ainsi que sur la dernière rangée externe des "pétales", sont couplés à des photomultiplicateurs Hamamatsu 5" de type R6594 à photocathode sphérique (Fig2.4) (900 PM).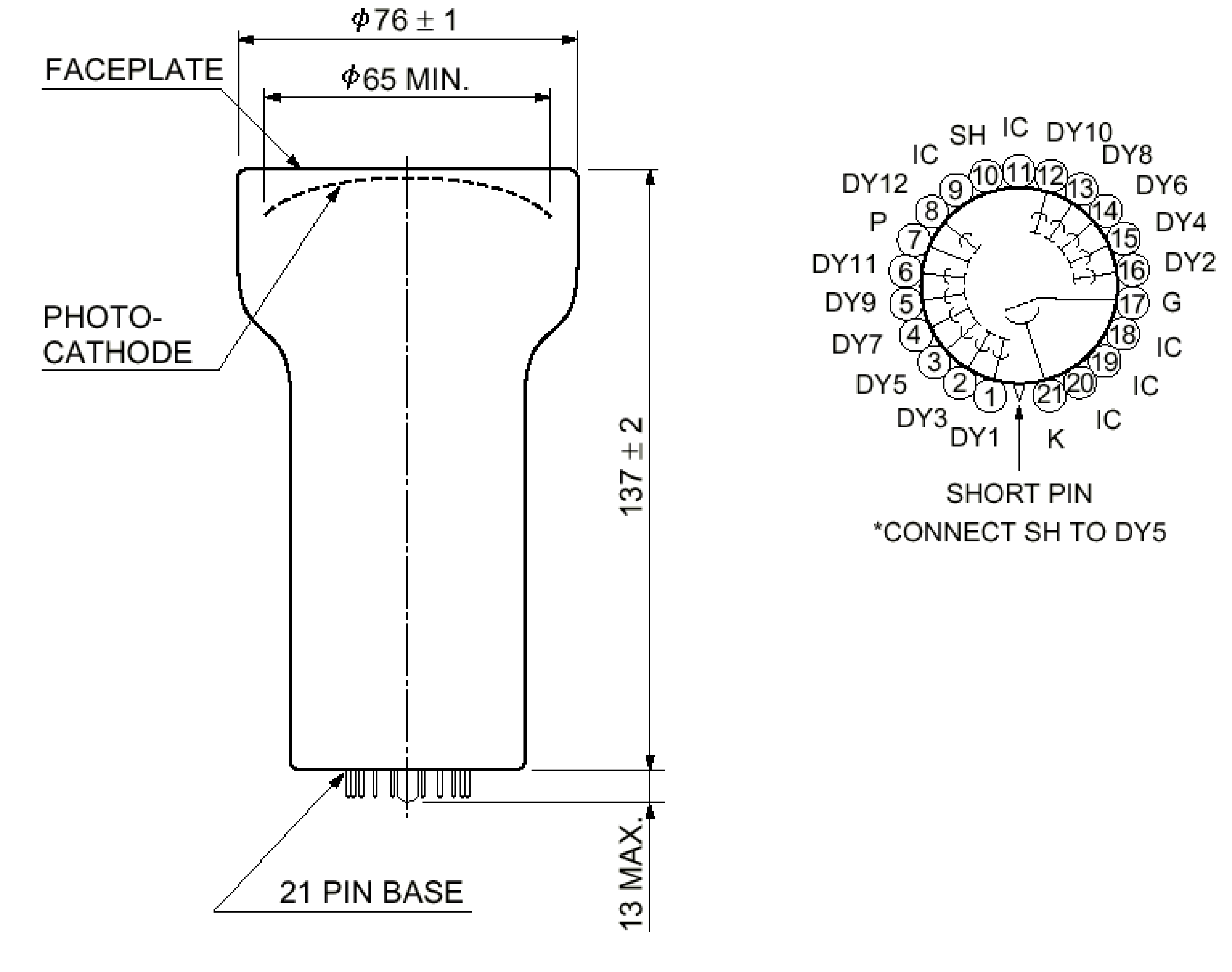
Les scintillateurs de plus petite dimension, localisés sur le mur interne et sur les 3 rangées restantes des "pétales", sont couplés à des photomultiplicateurs Hamamatsu 3" de type R6091 à photocathode plate (Fig2.5) (1040 PM). Tous ces photomultiplicateurs, de bas bruit de fond en $ {}^{40}$K,$ {}^{214}$Bi, et $ {}^{208}$Tl ont été conjointement développés par la firme Hamamatsu [7] et la collaboration NEMO. La production a duré 1 an et les spécifications électriques portaient essentiellement sur le rendement quantique de la photocathode ($ \sim$ 25%), son profil, le gain ( $ \sim 2.10^{6}$) , la linéarité de la réponse et le niveau de bruit de fond. Les hautes tensions moyennes sont respectivement de 1350 V pour les 5 pouces et 1800 V pour les 3 pouces. Le choix de la tension de fonctionnement à appliquer est déterminé lors d'une procédure dite d'alignement au cours de laquelle on s'assure que le signal électrique fourni corresponde à une charge de 125 pC pour un flux équivalent à 1 MeV.

Figure 2.5: Photomultiplicateur Hamamatsu 3" RS6091
\includegraphics[width=7cm height=6cm]{hama3.eps}

Les tableaux 2.1 et 2.2 rassemblent les activités mesurées et autorisées pour les photomultiplicateurs 5" et 3" [8].


Tableau 2.1: Activités des photomultiplicateurs Hamamatsu 5" type R6594
Activités (Bq/kg) $ {}^{214}$Bi $ {}^{208}$Tl
mesures 0.37 $ \pm$ 0.03 0.037 $ \pm$ 0.005
limite autorisée $ \leq$ 1.6 $ \leq$ 0.4



Tableau 2.2: Activités des photomultiplicateurs Hamamatsu 3" type R6091
Activités (Bq/kg) $ {}^{214}$Bi $ {}^{208}$Tl
mesures 0.27 $ \pm$ 0.03 0.029 $ \pm$ 0.004
limite autorisée $ \leq$ 1.3 $ \leq$ 0.3


Tous les scintillateurs sont recouverts sur les faces avant et latérales de deux couches de 6 $ \mu$m de mylar aluminisé (400 Å) et sur la face arrière d'une couche de 12 $ \mu$m de mylar aluminisé (1000 Å). Sur les faces latérales 5 couches de 70 $ \mu$m de téflon permettent d'optimiser la collection des photons de scintillation. Les photomultiplicateurs sont blindés contre le champ magnétique par du mu-métal. Un capot réalisé en matière plastique assure leur protection contre la lumière ambiante et permet en même temps un balayage d'azote qui limite les infiltrations d'hélium dans les photomultiplicateurs.

Les techniques d'identification des événements

L'association du détecteur de traces et des scintillateurs permet de classifier les événements enregistrés en fonction du nombre de traces que l'on peut reconstruire et du nombre de scintillateurs déclenchés. Ainsi, une trace reconstruite qui n'aboutit vers aucun scintillateur n'est d'aucune utilité et l'événement est rejeté. Les événements $ \beta\beta$ sont caractérisés par deux traces reconstruites chacune associée à un scintillateur déclenché. Les critères permettant d'analyser ces événements sont les suivants[9]:

-
le calcul du temps de vol permet de connaître le lieu de leur création. Nous pouvons ainsi distinguer les évènements $ \beta\beta$ des évènements à un électron en calculant un temps de vol théorique pour chacun des scénarios et en le comparant au temps de vol mesuré.

-
on fixe une coupure basse sur l'énergie déposée dans les scintillateurs. Elle dépend directement de la statistique désirée mais les tests montrent qu'en dessous de 100 keV, la résolution en temps se dégrade et les mesures de temps de vol ne sont plus fiables.

-
des coupures spatiales sont aussi effectuées sur la position du vertex et sur la distribution angulaire de la désintégration. Cette étude sera presentée dans la section 3.6.

Electronique d'acquisition

L'électronique d'acquisition du détecteur NEMO3 a été réalisée par le LPC de Caen en collaboration avec le groupe électronique du LAL. Elle est divisée en 40 modules (1 par demi-chambre à fils) qui gèrent indépendament les 360 signaux Geiger et les 50 signaux des compteurs. On distingue pour chacun d'eux:

-
Electronique du calorimètre: le déclenchement du signal "évènement photomultiplicateur" se fait en deux temps: le franchissement du seuil bas normalement fixé à 13 mV ($ \sim$ 40 keV) déclenche l'échelle des temps tandis que le franchissement du seuil haut déclenche l'intégration de la charge sur 80 ns. La présence de ce seuil bas permet d'éliminer une partie des signaux du bruit de fond. La charge est codée sur 4096 canaux pour une énergie maximale mesurée de 12 MeV. Le temps est lui aussi codé sur 4096 canaux avec une résolution de 220 ns.

-
Electronique de la chambre à fils: deux cartes dite T2 interne et T2 externe gèrent chacune les 180 signaux (internes et externes) des cellules Geiger. Pour chaque rangée de cellules, le signal anodique ainsi que les deux signaux cathodiques sont numérisés à travers un convertisseur TDC. Le temps entre le signal anodique et le déclenchement des photomultiplicateurs est égal 1.5 $ \mu$s tandis que la somme des temps cathodiques est proche de 80 ns[8]. Elles enverront au trigger central la configuration de déclenchement.

-
Trigger central: il permet de regrouper les informations des deux électroniques précédentes en essayant de repérer d'éventuelles coïncidence entre ces deux sous ensembles.

Pour les événements $ \beta\beta$ ou les événements à 1 électron comme ceux étudiés dans le chapitre 3, nous imposons, pour débuter l'intégration, qu'un compteur soit au moins touché (franchissement du seuil haut) et que 4 plans de cellules Geiger soient déclenchés dans une des deux demi-chambres à fils.

Calibrage en énergie du calorimètre NEMO3

Introduction

Durant la phase de prises de données, un test de calibration de chaque compteur est effectué. Ceci permet de mettre à jour dans la base de données la relation entre la charge déposée et l'énergie de l'électron. Cette relation est déterminante dans l'expérience NEMO3 car une erreur de 1% sur son énergie conduit à une erreur de 13% sur la demi-vie du processus $ \beta\beta(0\nu)$ du $ {}^{100}$Mo.
Cette opération peut être effectuée à l'aide d'un spectromètre à électrons avant la phase d'assemblage. Les tests réalisés montrent une résolution comprise entre 12 % et 16% (FWHM à 1 MeV)[10]. Cependant, malgré sa taille réduite, ce spectromètre ne peut pas être introduit dans le détecteur.

Solution adoptée pour la calibration en énergie de NEMO3

Il faut donc utiliser des sources radioactives produisant des électrons qui atteindront la face avant des blocs de scintillateurs. Les études sur le prototype NEMO2 ont montré qu'il était très difficile de positionner les sources radioactives directement en face des compteurs dans l'enceinte de gaz fermée. La solution choisie est alors de les mettre au niveau des feuilles sources de manière à reproduire au mieux la trajectoire des électrons. En utilisant le détecteur de traces avec le champ magnétique, nous pouvons être alors dans des conditions réelles d'acquisition. Il faut faire un compromis sur l'activité des sources: des sources de trop faible activité pourraient compliquer la procédure d'échantillonnage à long terme. De la même manière, des sources de trop forte activité augmenteraient le taux de déclenchement du trigger et produirait un bruit de fond beaucoup trop grand pour les événements attendus.

Description du protocole expérimental

Chaque secteur de NEMO3 comporte un tube d'étalonnage vertical au niveau de la feuille source équipé de trois fenêtres en kapton de 30 $ \mu$m d'épaisseur (Fig3.1). Pour pouvoir introduire les sources radioactives, nous utilisons une tige plastique de 3m de long, pliable en quatre morceaux. La tige dispose de 3 emplacements dans lesquels nous insérons les trois sources dans leur cadre en cuivre. Une fois équipés avec les trois sources, nous amenons la tige en haut des secteurs.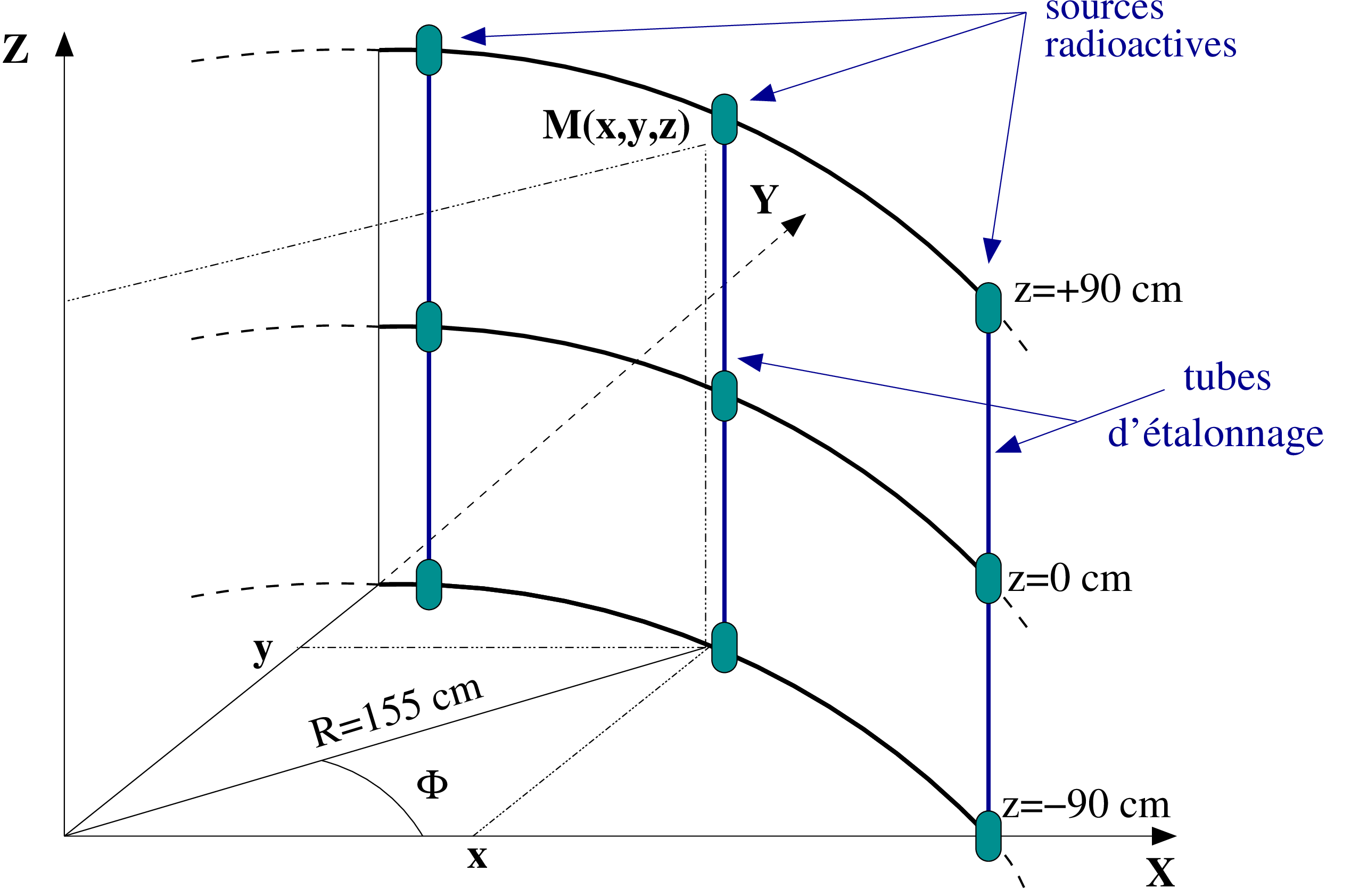

Figure 3.1: Schéma montrant la position des sources de calibration dans le détecteur NEMO3
\includegraphics[width=10cm height=8cm]{dessin_protocole.eps}

La mécanique du tube d'étalonnage permet de positionner la source dans la tige au niveau de chaque fenêtre en kapton avec une erreur de moins d'1 mm. Les trois sources sont donc placées respectivement au centre du tube (Z=0cm), en haut du tube (Z=90cm) et en bas du tube (Z=-90cm).

Sources radioactives

Des mesures effectuées à l'IreS avec un banc de test composé d'une lampe à hydrogène et de disques atténuateurs ont montré que la réponse des photomultiplicateurs était linéaire jusqu'à 4 MeV[11]. Il suffit donc de deux mesures d'énergie bien définies pour définir la courbe de calibration qui est de la forme: $ E=\alpha (canal_{ADC})+\beta$ où $ \alpha$ et $ \beta$ sont les deux paramètres à déterminer. La source de $ {}^{207}$Bi fournit principalement des électrons de conversion de 482 et 976 keV parfaitement adaptés à une calibration jusqu'à 1 MeV. Son schéma de désintégration[1] est représenté sur la figure 3.2. Nous pouvons distinguer les deux niveaux du noyau fils $ {}^{207}$Pb situés à 1633 keV et 570 keV: ils donnent un électron de conversion dont l'énergie et la probabilité de conversion dépendent de la couche K,L,M où ils sont émis[12].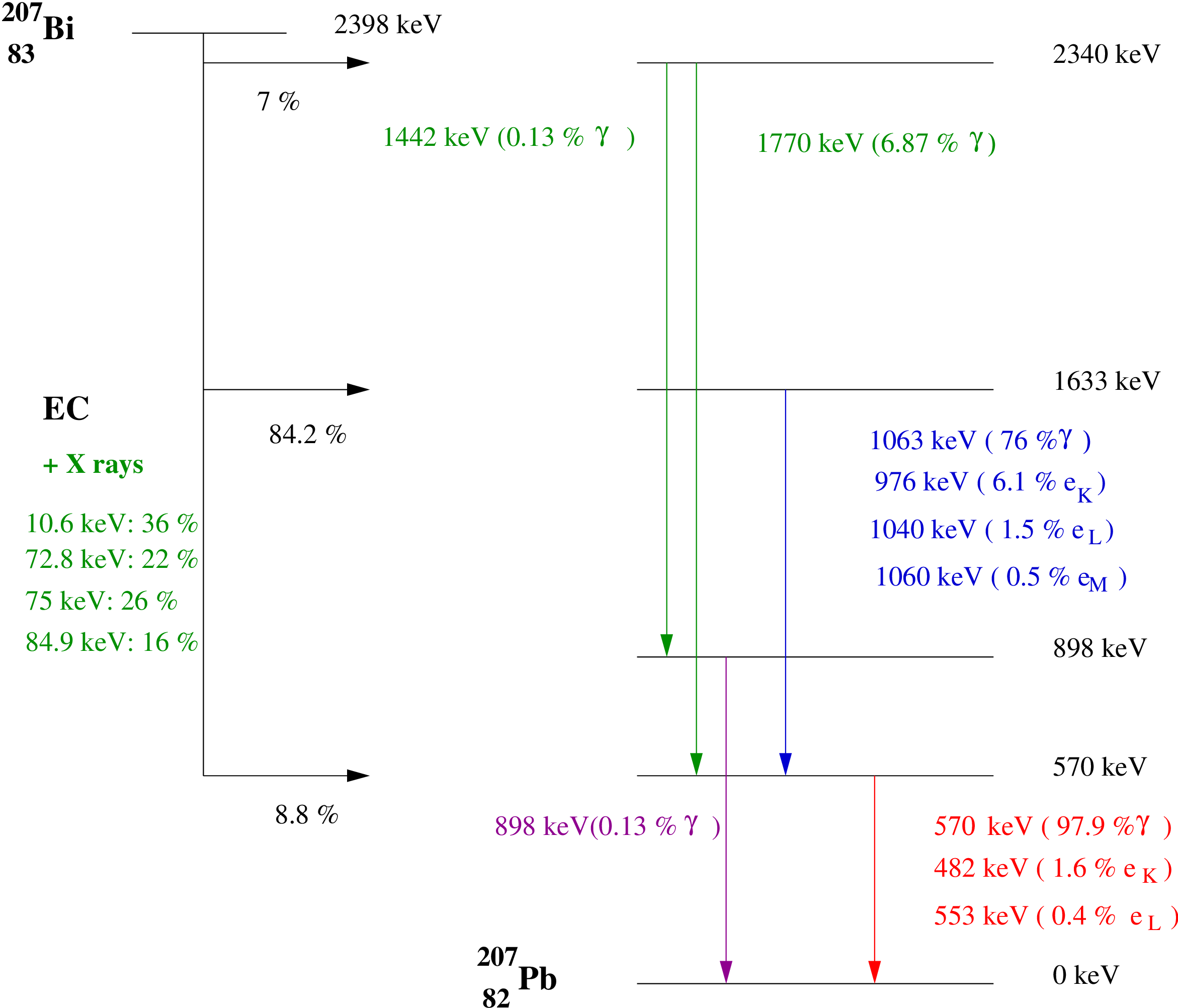

Figure 3.2: Schéma de désintégration du $ {}^{207}$Bi
\includegraphics[width=10cm height=10cm]{bi.eps}

Il faut être aussi capable de mesurer des énergies jusqu'à 3 MeV ( $ Q_{\beta\beta}$$ {}^{100}$Mo=3033 keV) ou plus (dans l'éventuelle présence d'un bruit de fond associé aux neutrons externes ou aux $ \gamma$). Il est prévu d'utiliser des sources bêta de $ {}^{90}$Y (fils du $ {}^{90}$Sr) et de $ {}^{106}$Rh (fils du $ {}^{106}$Ru)[13]. Elles permettent d'avoir dans la fin du spectre deux autres points de calibration ($ Q_{\beta}$=2.283 MeV pour $ {}^{90}$Y et $ Q_{\beta}$=3.540 MeV pour $ {}^{106}$Ru).

Dans les deux situations (électrons de conversion du $ {}^{207}$Bi et électrons bêta du $ {}^{90}$Sr et du $ {}^{106}$Ru), le problème de sélection des événements collectés est différent. La désintégration du $ {}^{207}$Bi produit essentiellement des raies $ \gamma$ de 570, 1063 et 1770 keV à travers tout le détecteur. Afin d'extraire les rares événements où le scintillateur a été touché par un électron de conversion et de s'assurer que cet électron provient directement de la source (sans diffuser sur un fil par exemple), le détecteur de traces doit être activé. En appliquant un modèle de reconnaissance sur les trajectoires, il est possible d'identifier les événements connus.

Au contraire, la calibration avec les sources de $ {}^{90}$Sr et de $ {}^{106}$Ru ne nécessite pas un modèle de reconnaissance car les événements cherchés sont situés dans la queue du spectre et ne peuvent venir que des sources.

La logique de déclenchement du trigger dans les deux types de calibration est aussi différente: dans le cas du $ {}^{207}$Bi, la présence de coups dans les cellules Geiger associés à un scintillateur touché avec une énergie déposée supérieure à environ 200 keV (cf Section 3.6) est nécéssaire pour déclencher l'intégration, ceci afin d'éliminer les coups associés aux électrons rétrodiffusés dans le scintillateur. Pour les électrons bêta, il suffit d'un scintillateur touché avec une énergie supérieure à 1 MeV ($ {}^{90}$Sr) ou 2 MeV ($ {}^{106}$Ru)[13]. Le second type de calibration permet d'utiliser des sources de plus grosse activité et d'avoir ainsi une fréquence d'acquisition plus élevée.

Etalonnage en temps

Nous avons vu dans la section 2.6.2 l'importance de la connaissance précise du temps de vol des particules dans la réjection du bruit de fond. L'étalonnage en temps comprend 3 étapes. La première étape consiste en un ajustement en temps des compteurs. En effet, l'électronique et le temps de transit des électrons dans les phototubes peuvent introduire des retards qui doivent être corrigés. Cette correction est effectuée à l'aide de données enregistrées avec une source de $ {}^{60}$Co qui émet deux $ \gamma$ en coïncidence.

Analyse des événements venant des sources $ {}^{207}$Bi

La calibration avec les sources de $ {}^{207}$Bi doit donc être effectuée avec le détecteur de traces de telle manière que les coups des cellules Geiger peuvent être utilisés pour reconstruire la trajectoire, après une sélection appropriée des événements collectés. En utilisant 60 sources de $ {}^{207}$Bi ayant chacune une activité de 6 nCi et avec un seuil haut de 50 mV($ \sim$ 160 keV), il est prévu de collecter entre 500 et 1000 événements pour chaque compteur[14]. Seuls les événements localisés sur un coté de la source et dans 2 secteurs consécutifs au maximum sont pris en compte. En dessous d'un certain seuil de probabilité, on rejette les coups déclenchés par des électrons secondaires diffusés à des grands angles dans le détecteur. L'intersection de la trajectoire reconstruite avec la surface cylindrique contenant les sources permet de localiser la source ayant produit l'électron détecté. Les traces passant relativement loin de la position des sources ainsi que les traces associées à des scintillateurs non déclenchés sont rejetées grâce à des coupures spatiales et temporelles.

Reconstruction des vertex

Il s'agit ici d'évaluer la précision sur la reconstruction du point d'émission situé dans l'une des 3 positions longitudinales (Z=-90,0,+90 cm). Le programme utilisé traite tous les événements collectés durant les runs. La figure 3.3 représente la distribution de la position des vertex associés aux événements avec une seule trace et un seul scintillateur de touché; le scintillateur est aussi corrélé à la trace.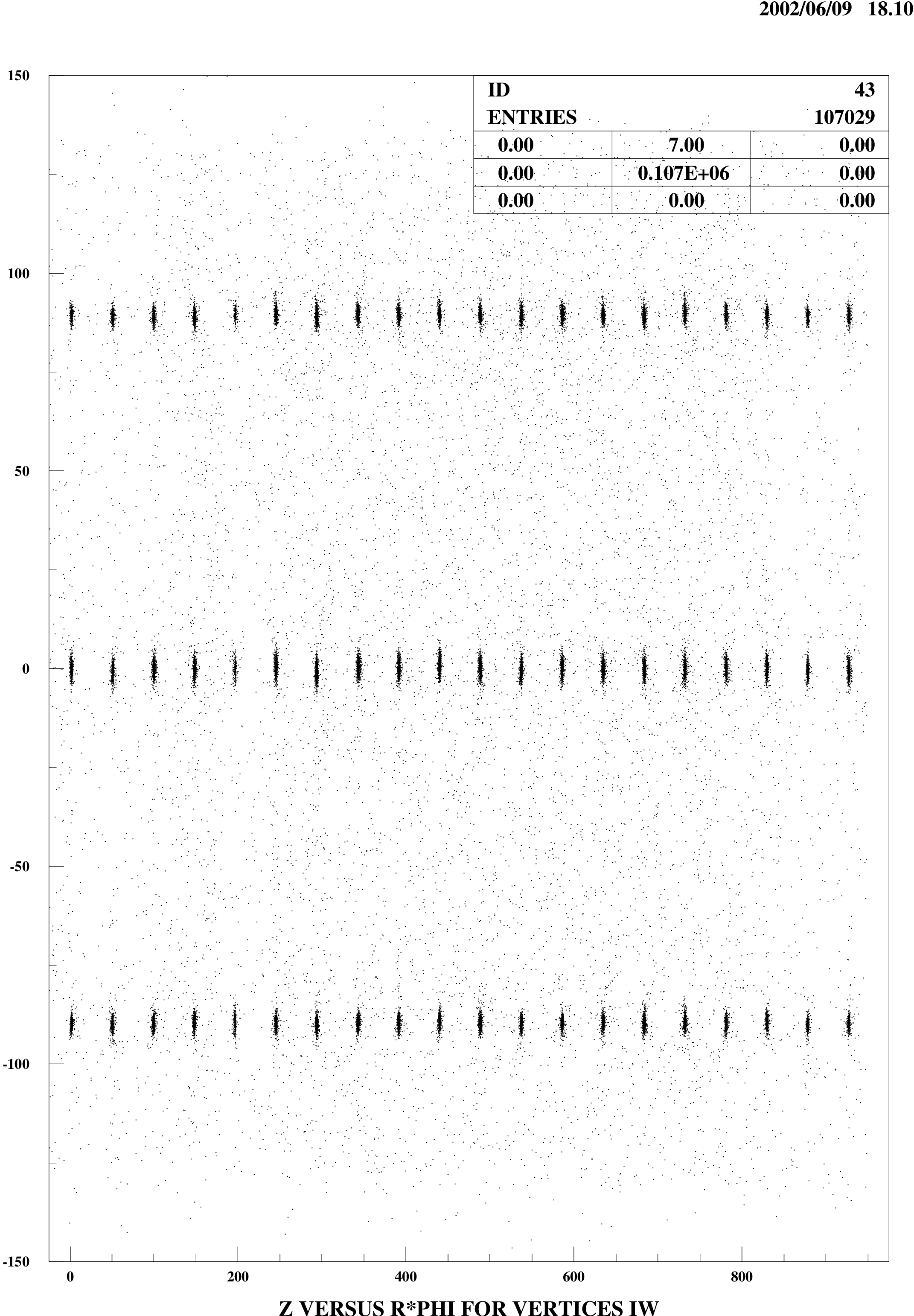

Figure 3.3: Carte des vertex reconstruits sur les feuilles sources des 20 secteurs en utilisant uniquement les compteurs internes
\includegraphics[width=8cm height=9cm]{vertex3.eps}

Nous distinguons pour chaque secteur(coordonnée R$ \phi$) les 3 zones d'émission qui correspondent aux 3 positions verticales des sources(coordonnée Z). Pour quantifier la largeur de la distribution autour des sources, nous avons ajusté les projections R$ \phi$ et Oz par une distribution gaussienne. La largeur de cette gaussienne pourra alors nous renseigner sur les coupures spatiales à appliquer. La figure 3.4 est un exemple de fit réalisé sur les données réelles acquises début Avril. Le bruit de fond est assimilable à une constante dans la région de l'ajustement.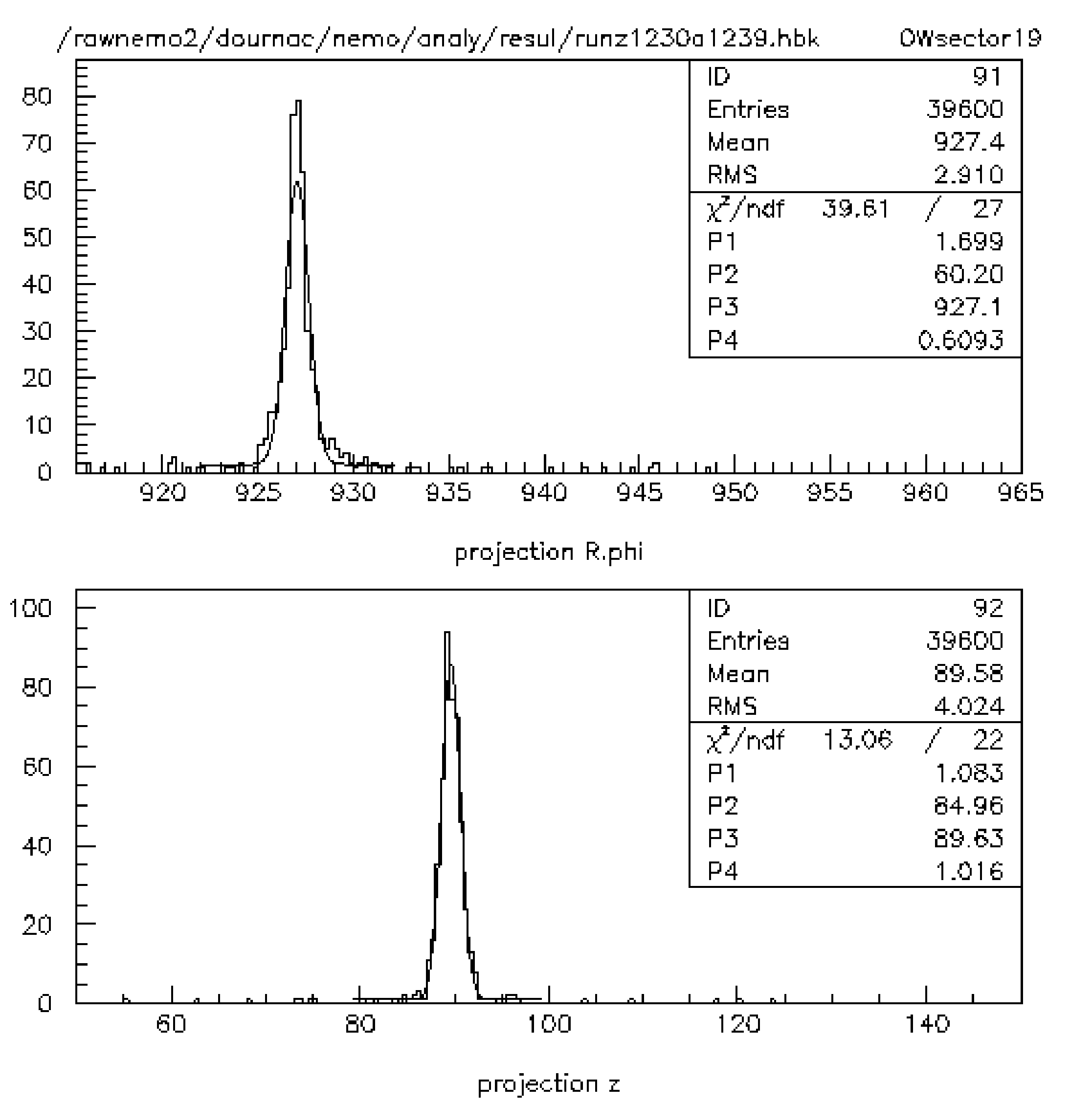

Figure: Distribution de la position longitudinale et transversale des vertex reconstruits sur les compteurs externes et ajustement par la fonction suivante: $ P1+P2 . exp^{\big(-\frac{(X-P3)^2}{2 P4^2}\big)}$
\includegraphics[width=9cm height=9cm]{fit1.eps}

Ces ajustements ont été réalisés pour chacune des 60 sources de $ {}^{207}$Bi et pour les trois parties du calorimètre (mur interne, externe, et les pétales). Les résultats sont résumés dans le tableau 3.1. Les 4 couronnes (haut et bas) sont numérotées dans l'ordre croissant du mur interne vers le mur externe. Nous remarquons que les résolutions obtenues en longitude sont supérieures à celles du plan Oxy. Ceci peut s'expliquer par plusieurs raisons: la cellule Geiger possède intrinsèquement une résolution moins bonne en Z (1cm).
Ceci peut aussi s'expliquer par les diffusions que peut subir l'électron sur le bord des fenêtres contenant les sources. Cette contribution apparaît sous la forme d'une gaussienne qui vient se rajouter aux 2 projections, donnant ainsi de nombreux événements sur les cotés qui sont visibles quand la résolution est bonne (cf projection R$ \phi$ sur la figure 3.4).


Tableau 3.1: Moyennes des résolutions longitudinales et transversales dans la reconstruction des vertex obtenus avec les 60 sources de $ {}^{207}$Bi
$ \langle \sigma \rangle (cm)$ $ \langle \sigma_{x} \rangle$ $ \langle \sigma_{y} \rangle $ $ \langle \sigma_{z} \rangle $
Mur interne 0.26 $ \pm$ 0.14 0.25 $ \pm$ 0.13 1.10 $ \pm$ 0.22
Mur externe 0.33 $ \pm$ 0.17 0.32 $ \pm$ 0.17 1.10 $ \pm$ 0.23
Couronne 1 0.20 $ \pm$ 0.10 0.21 $ \pm$ 0.11 1.02 $ \pm$ 0.14
Couronne 2 0.28 $ \pm$ 0.15 0.27 $ \pm$ 0.14 1.79 $ \pm$ 0.23
Couronne 3 0.28 $ \pm$ 0.15 0.28 $ \pm$ 0.15 1.65 $ \pm$ 0.25
Couronne 4 0.23 $ \pm$ 0.02 0.20 $ \pm$ 0.12 1.03 $ \pm$ 0.20


Pour vérifier la bonne reconstruction des vertex en Z, nous l'avons comparée avec la position réelle de la source connue au mm près en fonction des 3 positions de source et de chaque partie du détecteur (mur interne, externe et pétales). Les traces touchant les couronnes ne participent pas à la reconstruction des vertex situés au milieu du tube d'étalonnage (Z=0cm) et du coté opposé où elles se situent. En effet, une longue trace correspond à une importante perte d'énergie, ce qui accentue l'imprécision sur la position du point d'émission.
Cette vérification permet d'une part de contrôler d'éventuels défauts de construction mais aussi de valider l'algorithme de reconstruction des coordonnées en Z. Les résultats sont exposés dans le tableau 3.2. On remarque une dissymétrie entre les différentes positions indiquant un défaut dans l'algorithme de calcul des coordonnées des points d'impact des traces dans la chambre à fils.


Tableau 3.2: Ecarts moyens entre la position réelle et reconstruite pour les 60 sources de $ {}^{207}$Bi
$ \langle \Delta \rangle (cm)$ bas (-90cm) milieu (0cm) haut (90cm)
Mur interne -0.33 0.10 0.59
Mur externe -0.13 0.28 0.51
Couronne 1 0 - -0.5 10$ ^{-2}$
Couronne 2 0.91 - 1.20
Couronne 3 0.39 - 1.27
Couronne 4 0.17 - 0.23


Calibration dans le canal 1 électron

Le spectre attendu du $ {}^{207}$Bi doit comporter les 2 pics correspondant aux deux lignes prépondérantes des électrons de conversion émis (482 et 976 keV). La figure 3.5 représente le spectre obtenu avec l'ensemble des PM du calorimètre en cumulant les runs de $ {}^{207}$Bi effectués en Avril 2002. Evidemment comme nous avons cumulé l'ensemble des réponses des photomultiplicateurs, la résolution est légèrement détériorée.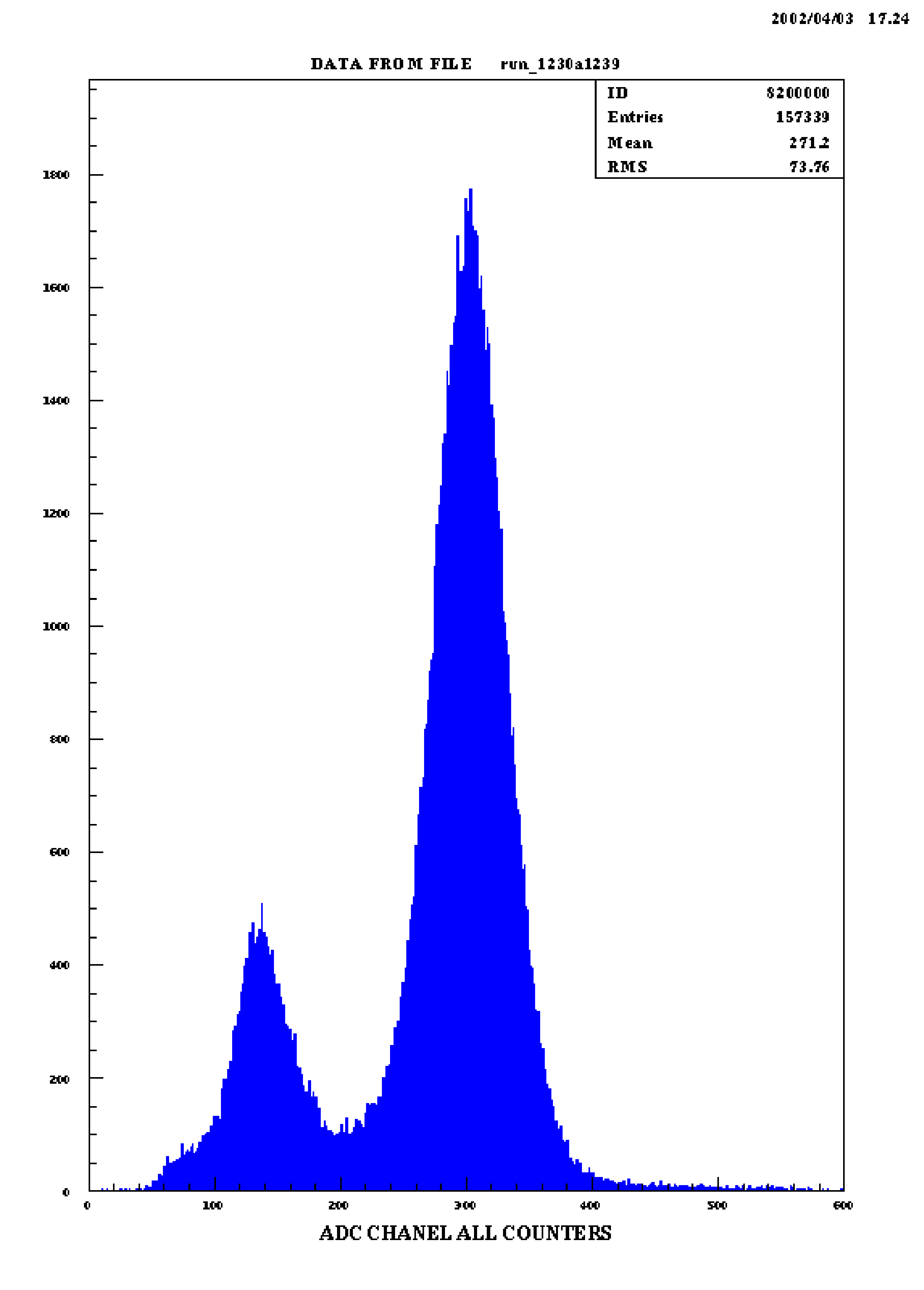

Figure 3.5: Spectre en énergie du $ {}^{207}$Bi dans le canal 1 électron pour l'ensemble des PM du calorimètre
\includegraphics[width=10cm height=8cm]{bispectre.eps}

Les deux pics sont clairement visibles. Ce run contient 1068449 événements. Le déclenchement du trigger se fait quand un événement du type "(1 électron + rayon X)" ou "(1 électron + rayon X) et rayon $ \gamma$" est identifié. Cette stratégie de trigger permet d'accumuler plus de statistique qu'avec l'événement "(1 électron + rayon X)" car l'électron de conversion peut être accompagné d'un $ \gamma$. En cumulant les probabilités, nous pouvons dire que dans 10.1% des cas (8.1%+2%), le $ {}^{207}$Bi émet "1 électron + 1X". Le nombre d'entrée de ce spectre représente 14.72% du nombre total d'événements. Cet écart s'explique par la présence d'électrons diffusés par les cavités en cuivre et les fenêtres entourant les sources. Des photons peuvent aussi diffuser par effet Compton (2 $ \gamma$ de 1063, et 570 keV et un de 1770 keV qui est négligeable) et produirent des électrons qui apparaissent sur tout le spectre. Le trigger impose la présence de hits dans la chambre à fils pour enregistrer l'événement.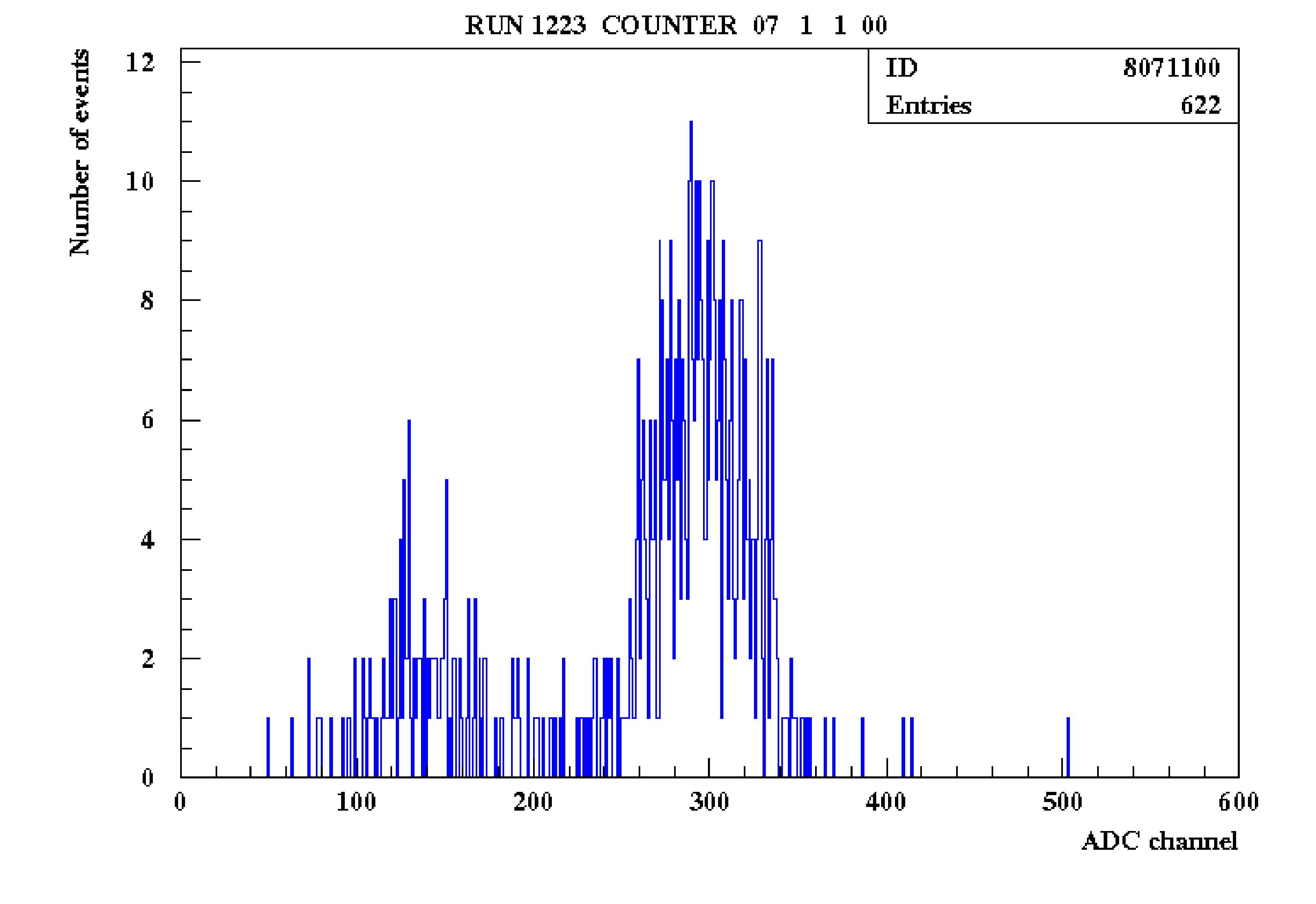

Figure 3.6: Spectre en énergie du $ {}^{207}$Bi dans le canal 1 électron pour 1 photomultiplicateur du mur externe
\includegraphics[width=12cm height=8cm]{spectrePM.eps}

Le but étant de calibrer chaque compteur, nous disposons d'un fichier contenant les événements pour chacun d'eux. Ce fichier contient le spectre du $ {}^{207}$Bi avec une statistique beaucoup plus faible (Fig3.6). Un programme permet de déterminer la pente de calibration en ajustant chacun des 2 pics par une somme de 3 gaussiennes dont les amplitudes et les largeurs relatives sont fixées en fonction des rapports d'intensité connues entre les couches K,L et M[12]. La relation "canal ADC - Energie" doit aussi tenir compte de l'énergie perdue par l'électron durant son temps de vol. En effet, l'électron traverse différents matériaux comme le support des sources en mylar, la fenêtre en kapton, le mélange gazeux hélium alcool et l'enveloppe des scintillateurs. Grâce à la trajectoire des traces obtenue avec la chambre à fils, on peut estimer l'énergie totale perdue par les électrons (entre 40 et 80 keV) et décaler ainsi la position des deux pics pour finalement obtenir les coefficients de calibrage. Un "rebinning" est effectué pour ajuster interactivement le spectre si le nombre d'entrées est trop faible. Ceci arrive sur les PM qui ne comptent pas beaucoup. Ces contraintes nous amène finalement à avoir 3 paramètres libres pour chacun des pics: la position et la largeur de la ligne K ainsi qu'une constante de normalisation. Un exemple de fit réalisé à partir des données réelles d'Avril est montré sur la figure 3.7. La courbe en bleu représente la droite de calibration "brute" (ajustée seulement avec les 2 pics) et la courbe en rouge représente la même droite mais ajustée sur 3 points (nous imposons de passer le plus près du point (0,0)).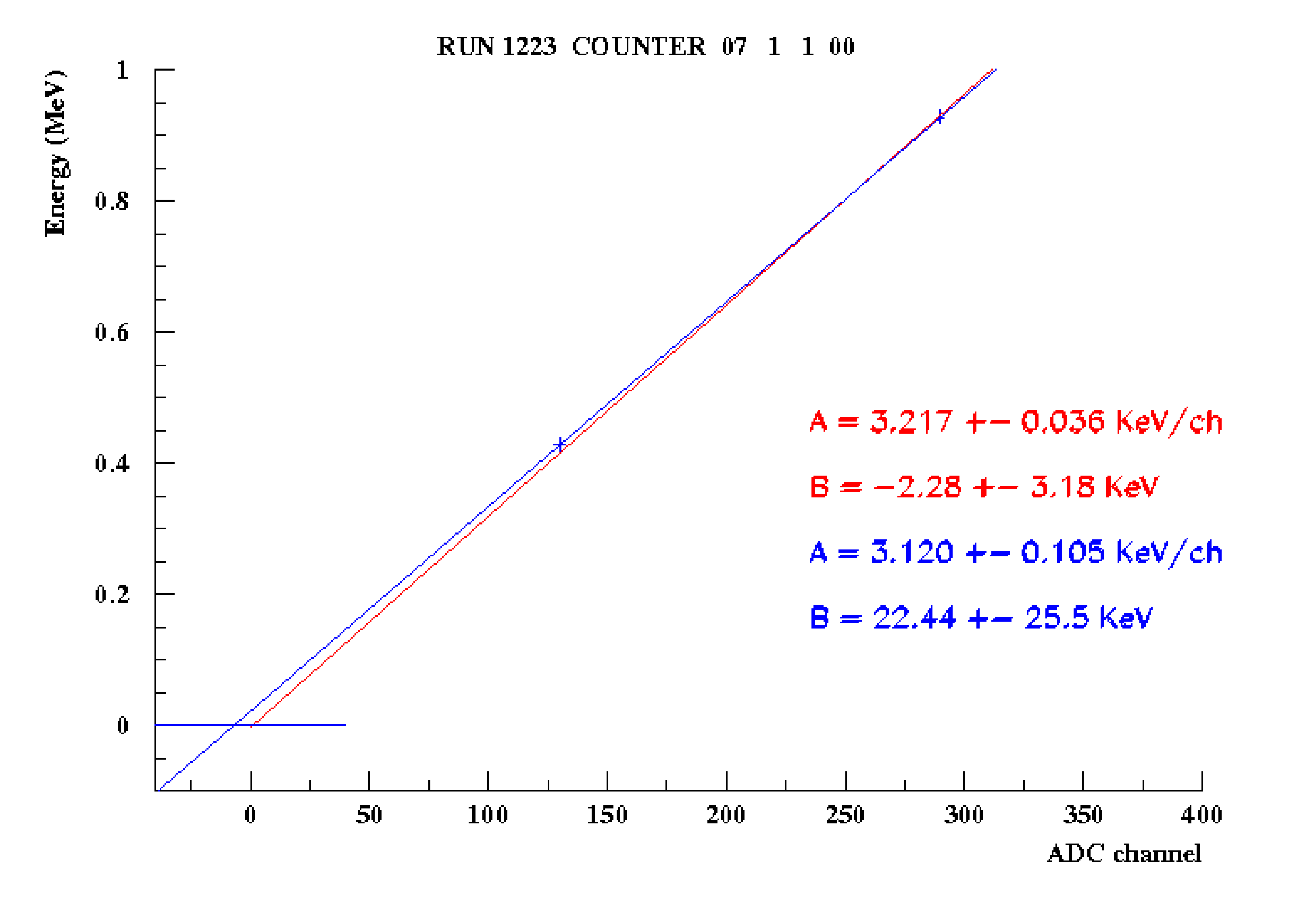

Figure 3.7: Résultats de calibration $ {}^{207}$Bi pour 1 photomultiplicateur
\includegraphics[width=12cm height=8cm]{fitpmbi.eps}

La résolution moyenne obtenue (FWHM) à partir du $ {}^{207}$Bi pour les 1919 compteurs ayant pu être traités à la suite des runs d'Avril 2002 est égale à 17$ \pm$1% pour le pic à 976 keV et à 29$ \pm$6% pour le pic à 482 keV. Ces runs ont été réalisés dans d'assez mauvaises conditions (problème de trigger). En temps normal, la collaboration espère, d'après les tests effectués atteindre une résolution d'au moins 14% à 1 MeV. On vérifie bien que la résolution varie approximativement en $ \frac{17}{\sqrt{E}}$, où $ E$ est l'énergie de l'électron (exprimée en MeV).

Analyse des événements venant des sources $ {}^{90}$Sr

La méthode précédente pour sélectionner les électrons pourrait être appliquée au cas du $ {}^{106}$Ru et au $ {}^{90}$Sr. Mais les cellules Geiger ne peuvent fonctionner correctement que si la fréquence d'acquisition est inférieure à 30 Hz. Or, pour obtenir une statistique suffisante dans la région de la queue du spectre, il faut utiliser des sources relativement actives (Les 4 sources utilisées en Avril avaient une activité de 200 nCi chacune). Une calibration utilisant uniquement les scintillateurs est donc recommandée. Avec un seuil haut fixé à 450 mV ($ \sim$ 1.5 MeV), il est prévu d'acquérir entre 500 et 1000 événements pour chaque compteur[14].

Calibration dans le canal 1 électron

Durant la séance de calibration d'Avril 2002, nous nous sommes seulement servi de la source bêta $ {}^{90}$Y (fils du $ {}^{90}$Sr) ayant un $ Q_{\beta}$ égal à 2.283 MeV. Nous avons utilisé 4 sources de $ {}^{90}$Sr que l'on a disposées dans le détecteur. Un roulement sur les positions permet de couvrir l'ensemble des secteurs. L'acquisition d'événements se fait quand un seul compteur est touché (canal 1 électron) et uniquement sur les deux secteurs voisins à la source.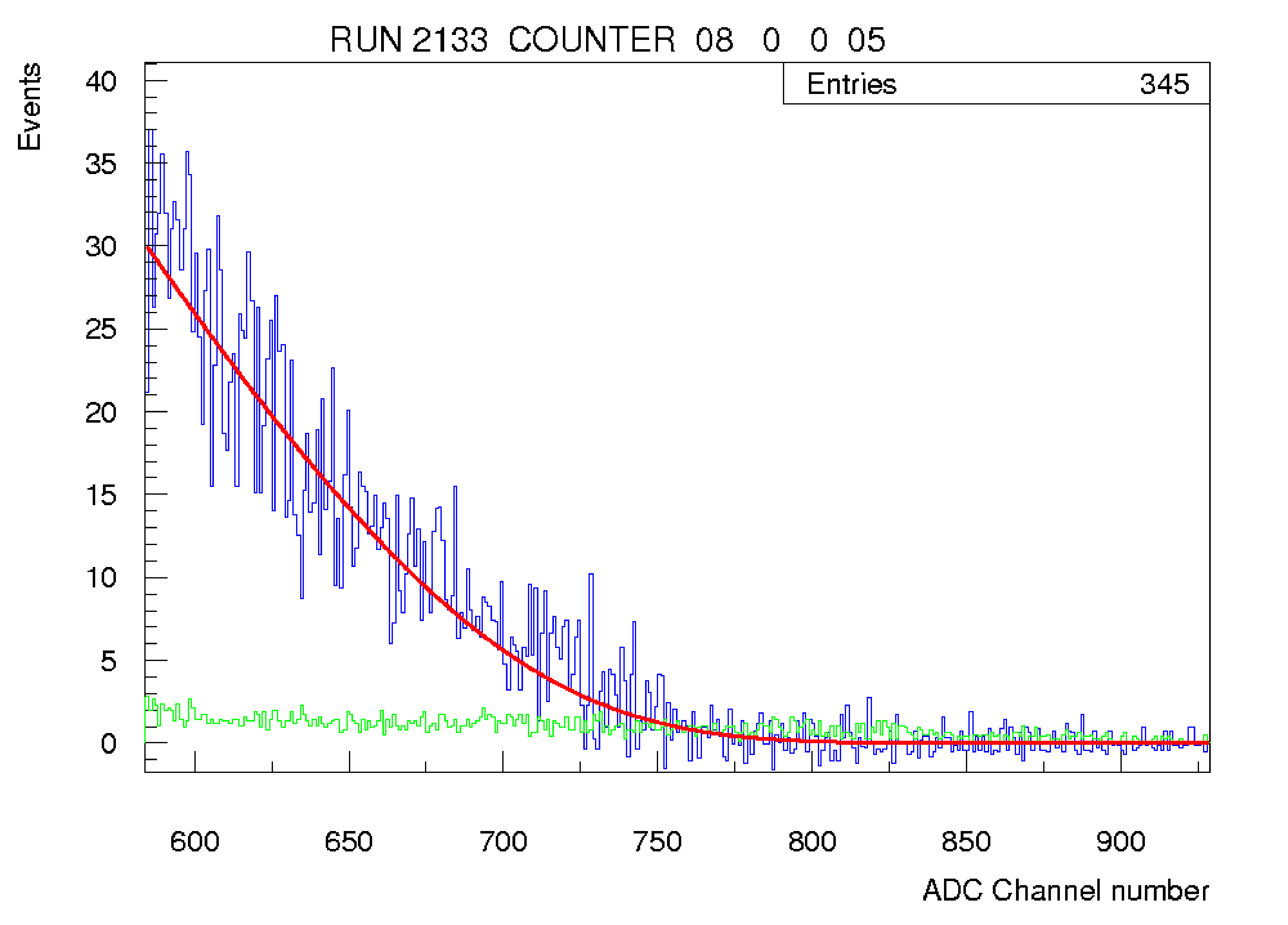

Figure 3.8: Exemple de fit sur la queue du spectre $ \beta$($ {}^{90}$Y)
\includegraphics[width=10cm height=10cm]{sr.eps}

Etant donné que le $ {}^{207}$Bi nous fournit une calibration jusqu'à 1 MeV, nous nous intéressons à la fin du spectre bêta (entre 1.5 et 2.5 MeV). Le programme que j'ai utilisé permet de paramétriser le spectre brut par une fonction représentant le spectre théorique du $ {}^{90}$Y convoluée par la fonction de résolution en énergie obtenue avec le $ {}^{207}$Bi (proportionnelle à $ \frac{1}{\sqrt{E}}$). Nous obtenons ainsi la pente de calibration sur le spectre $ \beta$. Une prise de données spéciale (sans sources) a permis d'estimer le bruit de fond pour pouvoir le soustraire du spectre obtenu avec sources. L'énergie moyenne perdue par l'électron peut être évaluée par simulation Monte Carlo pour chaque compteur en fonction de sa position relative par rapport aux sources: elle est estimée à environ 80 keV. Un exemple de fit réalisé à partir de données réelles se trouve sur la figure 3.8. La courbe en vert représente l'estimation du bruit de fond tandis que la courbe en rouge représente l'estimation du signal $ \beta$. L'histogramme en bleu représente le spectre après soustraction du bruit de fond. De cet ajustement, nous obtenons le coefficient $ \alpha$ de la pente de calibrage Energie-canal ADC ainsi qu'une constante de normalisation pour ramener la statistique du spectre théorique à celle du spectre obtenu (la valeur de $ \beta$ est fixée à celle obtenue avec le $ {}^{207}$Bi). J'ai réalisé ces ajustements pour l'ensemble des compteurs disponibles en cumulant les 5 runs de strontium réalisés en Avril (1734 PM sur 1940). Les coefficients pour chaque photomultiplicateur sont stockés dans un fichier qui sera réutilisé par la suite pour y appliquer les corrections lasers qui font l'objet du paragraphe suivant.

Corrections lasers

Un suivi permanent du gain des photomultiplicateurs est assuré par un système de contrôle laser. Ce système permet de délivrer des signaux analogues, en amplitude et en forme, aux impulsions données par les électrons ou les gamma dans les scintillateurs. Il est capable de détecter des variations de gain avec une résolution de l'ordre de 1% actuellement. Ce système va nous permettre dans un premier temps de vérifier les grosses variations de gain observées sur certains photomultiplicateurs entre les runs de Bismuth et de Strontium. Nous pourrons dans un deuxième temps tester l'efficacité de cette correction en la comparant à la distribution non corrigée.

Description du dispositif

Le système laser a été construit dans le but de pouvoir suivre l'étalonnage en temps et en énergie des photomultiplicateurs. La source de photons utilisée est un laser pulsé à azote émettant une lumière monochromatique de 337 nm. La quantité de lumière (150$ \mu$J par impulsion) est suffisante pour contrôler l'ensemble des 1940 compteurs du calorimètre de NEMO3 jusqu'à une énergie de 12 MeV.
Cette lumière laser traverse tout d'abord un filtre atténuateur variable (fig 3.9) qui permet de corriger d'éventuelles fluctuations d'énergie. Le faisceau est ensuite envoyé dans deux directions différentes :

-
vers une photodiode, connue pour son temps de montée rapide et pour sa stabilité à long terme. Elle sert de référence pour déterminer la relation temps énergie et permet de contrôler l'intensité de la lumière laser. Dans ce dernier cas, nous pouvons, avant d'envoyer la lumière laser vers les compteurs de NEMO3, agir sur le premier filtre atténuateur variable pour modifier la quantité de lumière.
-
vers un jeu de disques contenant des filtres atténuateurs discrets qui permettent de faire varier la quantité de lumière laser envoyée vers les compteurs dans un intervalle d'énergie compris entre 0 et 12 MeV.

Figure 3.9: Schéma du système laser de calibration relative
\includegraphics[width=15cm height=10cm]{laser.eps}

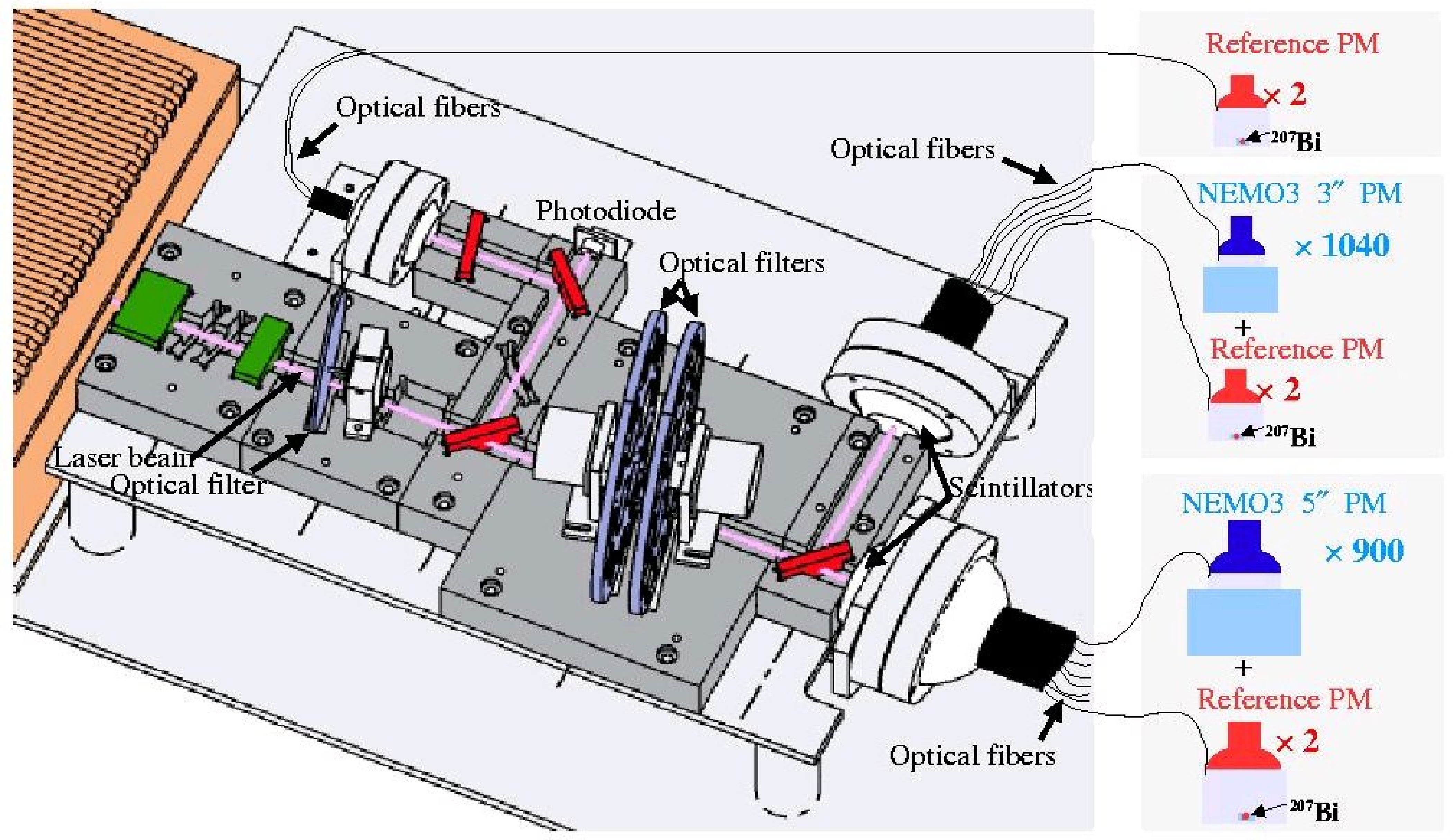Une position "0 MeV" corrrespond au blocage de l'envoi de la lumière laser vers les compteurs de NEMO3 et permet de monitorer la quantité de lumière laser avec la photodiode sans interrompre l'acquisition des événements.
Après ces deux disques atténuateurs, la lumière est à nouveau divisée en deux vers deux boules de scintillations (1 pour les compteurs 3" et 1 pour les 5") qui servent à modifier le signal pour qu'il ait les mêmes caractéristiques que la lumière émise par les scintillateurs de NEMO3 recevant des électrons: la longueur d'onde, le temps de montée de l'impulsion et sa largeur à mi-hauteur. La lumière est ainsi décalée à 420 nm et grâce aux multiples reflexions dans les boules de scintillations, la forme des impulsions laser est également modifiée. Sur ces boules sont collées les fibres optiques qui distribuent la lumière à l'ensemble du calorimètre de NEMO3. Les fibres utilisées sont des fibres plastiques d'environ 12 m de longueur qui ont été choisies pour leur faible coût et une bonne résistance à la casse. Elles sont en fait coupées en deux parties reliées entre elles par un système mécanique appelé équilibreur. Cet équilibreur permet de jouer sur la distance séparant les deux parties de la fibre, et ce, afin de corriger les variations de charges mesurées entre les différents compteurs. Il est effectivement possible de mesurer des quantités de lumière différentes dûes par exemple à un mauvais contact de la fibre avec le guide de lumière des photomultiplicateurs. Pour garantir la précision souhaitée sur le contrôle des variations de calibration, 6 photomultiplicateurs de référence sont utilisés dans ce système laser: 2 pour la photodiode, et 2 derrière chacune des 2 boules de scintillateur. Ces compteurs de référence sont eux-mêmes contrôlés chacun par une source de $ {}^{207}$Bi. En comparant la position du pic laser à celle dûe aux électrons de la source, on peut ainsi déterminer les variations d'intensité de la lumière laser.

Résultats

Un run laser a été effectué entre chaque run de $ {}^{207}$Bi et entre chaque changement de position de sources pour les runs de $ {}^{90}$Sr. Les données relatives aux corrections laser sont accessibles à travers le serveur principal MySQL de la base de données de NEMO situé au CCin2p3 à Lyon.

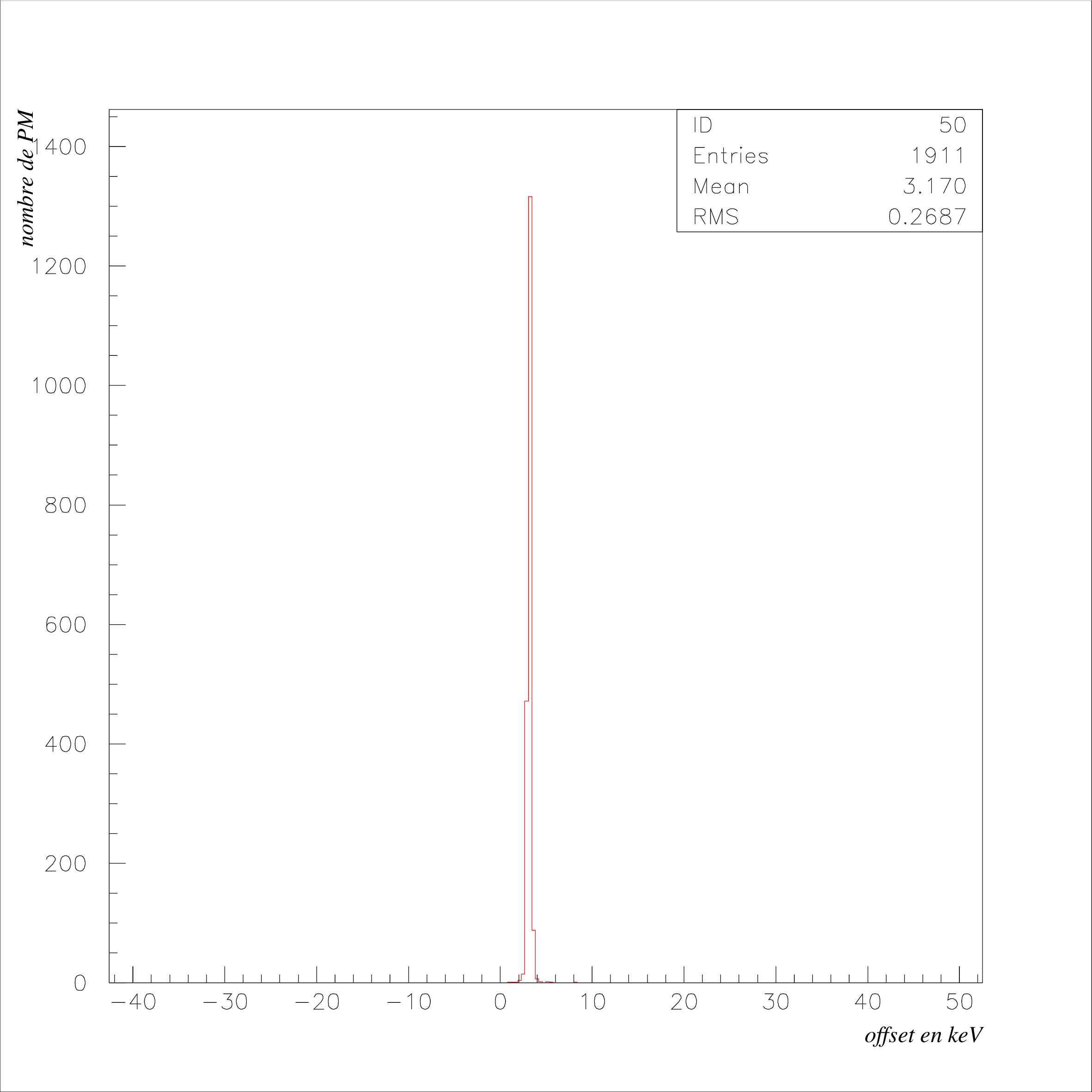
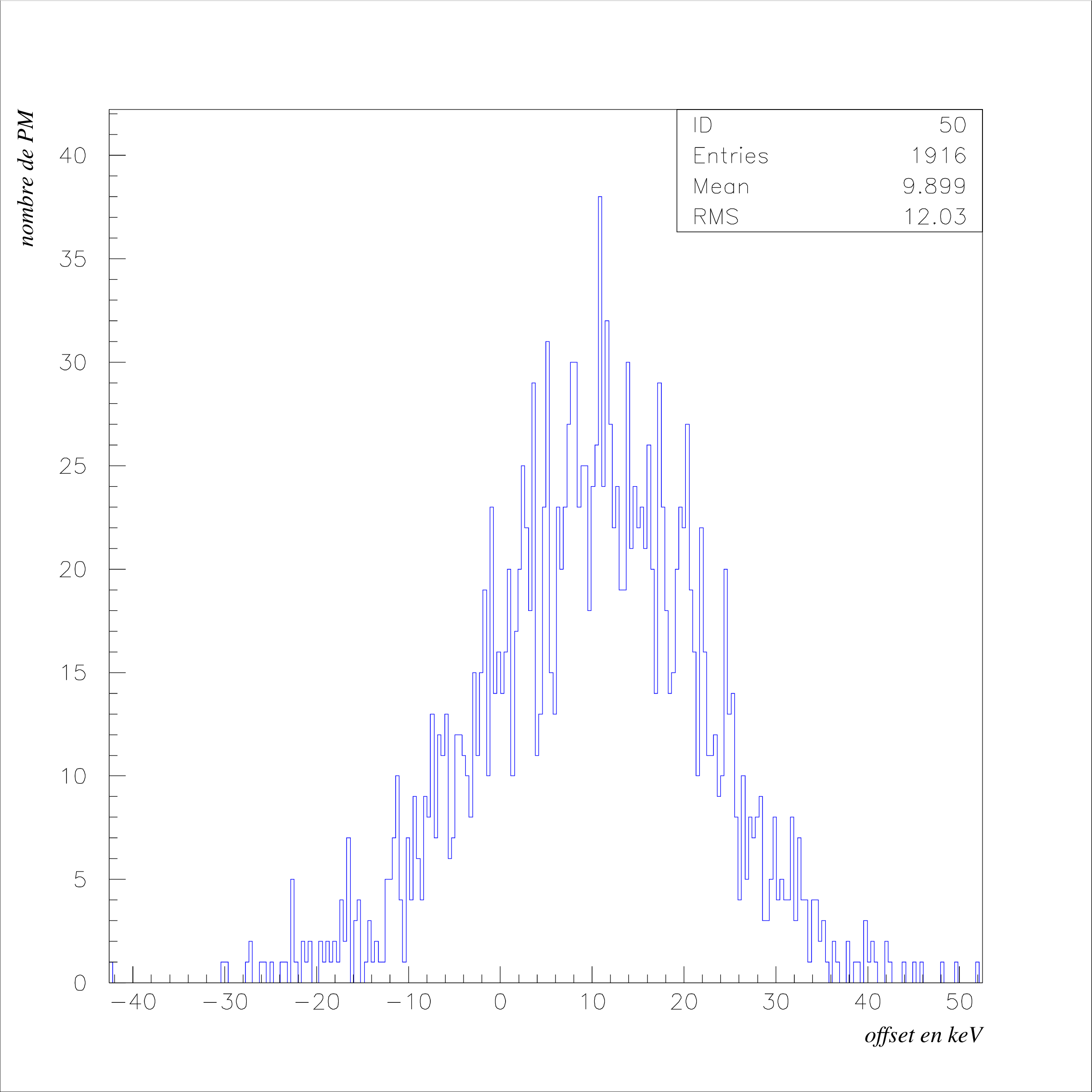
\fbox{ \begin{minipage}{0.5\textwidth} \begin{eqnarray} (\alpha)_{correction}=(\... ...}{E_{ run}}\bigg) \\ \phantom{rouge} \nonumber \end{eqnarray}\end{minipage}}


Pour chaque photomultiplicateur, les coefficients de calibrage précédents du $ {}^{207}$Bi et du $ {}^{90}$Sr sont corrigés en fonction du run de référence selon la formule (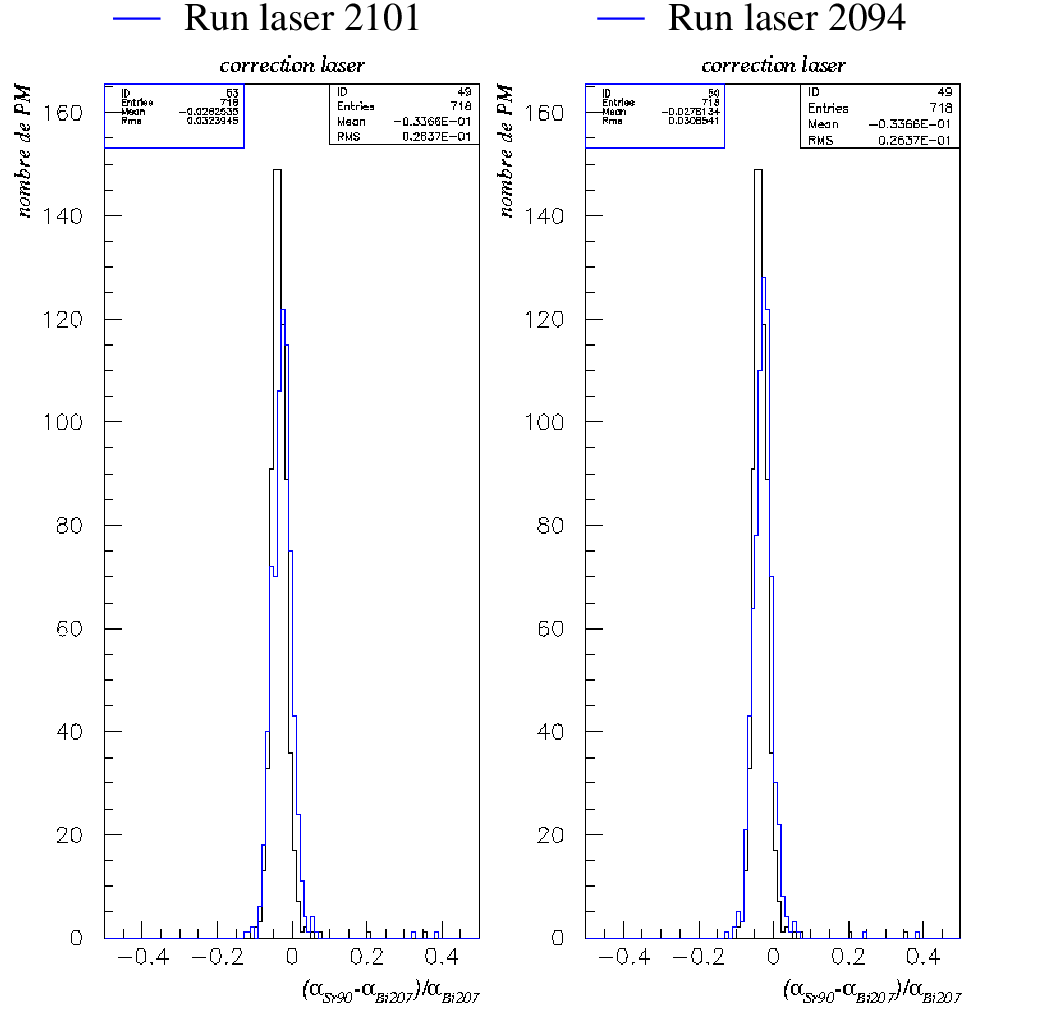3.1).


Figure 3.10: Comparaison entre la distribution non corrigée et corrigée de la pente de calibrage
\includegraphics[width=15cm height=16cm]{ex2.eps}

Cette opération a été réalisée pour chacun des 718 PM possédant une correction laser pour les runs $ {}^{207}$Bi et $ {}^{90}$Sr. Nous présentons les résultats pour deux runs lasers différents (Fig3.10). Les runs laser du $ {}^{207}$Bi, réalisés en premier, sont considérés dans notre calibration comme des runs de référence. En effet, par la suite, des problèmes de trigger relatifs aux cartes d'alimentation des photomultiplicateurs de référence sont intervenus, ce qui a obligé la collaboration à couper la haute tension sur ces compteurs. Nous avons représenté la variation relative de la pente obtenue entre les runs $ {}^{207}$Bi et $ {}^{90}$Sr. Nous remarquons tout d'abord que le gain des photomultiplicateurs a augmenté entre les deux runs ( $ \alpha_{Bi}>\alpha_{Sr}$). Ceci peut s'expliquer par le fait que les runs de $ {}^{90}$Sr ayant été réalisés après ceux du $ {}^{207}$Bi, les PM auraient atteint progressivement leur régime de fonctionnement. Nous voyons que la correction a pour conséquence de déplacer la distribution non corrigée vers 0, ce qui était bien attendu en supposant que la majorité des photomultiplicateurs sont restés stables entre les runs de $ {}^{207}$Bi et de $ {}^{90}$Sr. La largeur est par contre plus grande. Cet effet peut s'expliquer par la précision du système laser qui était alors du même ordre de grandeur que la moyenne obtenue, c'est à dire de 2 à 3%.

Distribution de l'offset

L'idée est ici d'essayer de savoir si l'offset, déduit des ajustements précédents, possède une signification physique dans le fit réalisé à la section 3.6. Nous pourrons ainsi valider la méthode utilisée pour le $ {}^{207}$Bi.

Figure 3.11: Distribution de l'offset obtenu à partir des runs de $ {}^{207}$Bi: en rouge le fit "forcé" (3 points) et en bleu le fit sur deux points
\includegraphics[width=8cm]{save_beta_force.eps} \includegraphics[width=8cm]{save_beta_non_force.eps}

Pour faire cette analyse, nous allons sur la distribution de l'offset issu du fit "non forcé" du $ {}^{207}$Bi (Section 3.6), sélectionner les compteurs par tranches successives et comparer relativement les distributions corrigées et non corrigées de leur pente de calibrage $ \alpha$. Sur la figure 3.11 est représentée la distribution de cet offset à la fois pour l'ajustement forcé et pour l'ajustement sur deux points. Pour l'ajustement sur deux points, la moyenne est légèrement décalée vers la droite, ce qui signifie qu'au "canal ADC" 0 correspond un offset moyen de 10 keV dans la relation de calibrage.

Si nous regardons l'effet de la correction laser sur différentes régions de cette distribution (cf Fig3.12,3.13 et 3.14) , nous remarquons que la correction a globalement le même ordre de grandeur quelque soit la tranche prise. Il y a donc une certaine indépendance de la correction sur le paramètre $ \beta$. Le run laser 2101 est légèrement plus efficace pour déplacer la correction ( $ \Delta_{\mu}$) car nous corrigons à la fois le Bismuth et le Strontium. Nous voyons de nouveau l'élargissement de la distribution pour les 2 runs de correction (de l'ordre de 0.5 %), ce que nous avons expliqué dans le chapitre précédent par la précision limitée du sytème laser. Les résultats sont résumés par les tableaux 3.3 et 3.4.


Tableau 3.3: Ecarts pour le run laser 2094
$ \Delta(\%)_{correction}$ $ \Delta_{\mu}$ $ \Delta_{\sigma}$
$ -5<\beta<5 keV$ 0.65 0.43
$ 5<\beta<15 keV$ 0.72 0.53
$ 15<\beta<25 keV$ 0.57 0.4



Tableau 3.4: Ecarts pour le run laser 2101
$ \Delta(\%)_{correction}$ $ \Delta_{\mu}$ $ \Delta_{\sigma}$
$ -5<\beta<5 keV$ 0.75 0.32
$ 5<\beta<15 keV$ 0.87 0.81
$ 15<\beta<25 keV$ 0.79 0.48


Ceci valide la façon dont l'ajustement des deux points du $ {}^{207}$Bi a été réalisé à la section 3.6. En effet, l'incertitude sur la perte d'énergie de l'électron (20 keV) rend à basse énergie la relation linéaire "Energie-canal ADC" imprécise. Le programme utilisé nous permettait de forcer en dessous d'une certaine erreur la droite de calibration à passer le plus près du point (0,0) ou simplement d'ajuster avec les positions des 2 pics du $ {}^{207}$Bi. A la suite de ces résultats, nous voyons en considérant que la résolution est de la forme $ \sqrt{\alpha \times E(keV)}$, que l'une n'est pas significative par rapport à l'autre, la correction ayant le même effet quelque soit l'offset. Il est prévu de déterminer pour les ajustements faits sur le Bismuth, une relation de calibrage plus précise à basse énergie en utilisant une fonction de résolution de la forme:

$\displaystyle \sigma(E)=\sqrt{\alpha \times E +\frac{\beta}{E^2}}$ (3.2)

où $ \alpha$ et $ \beta$ sont les deux paramètres à déterminer.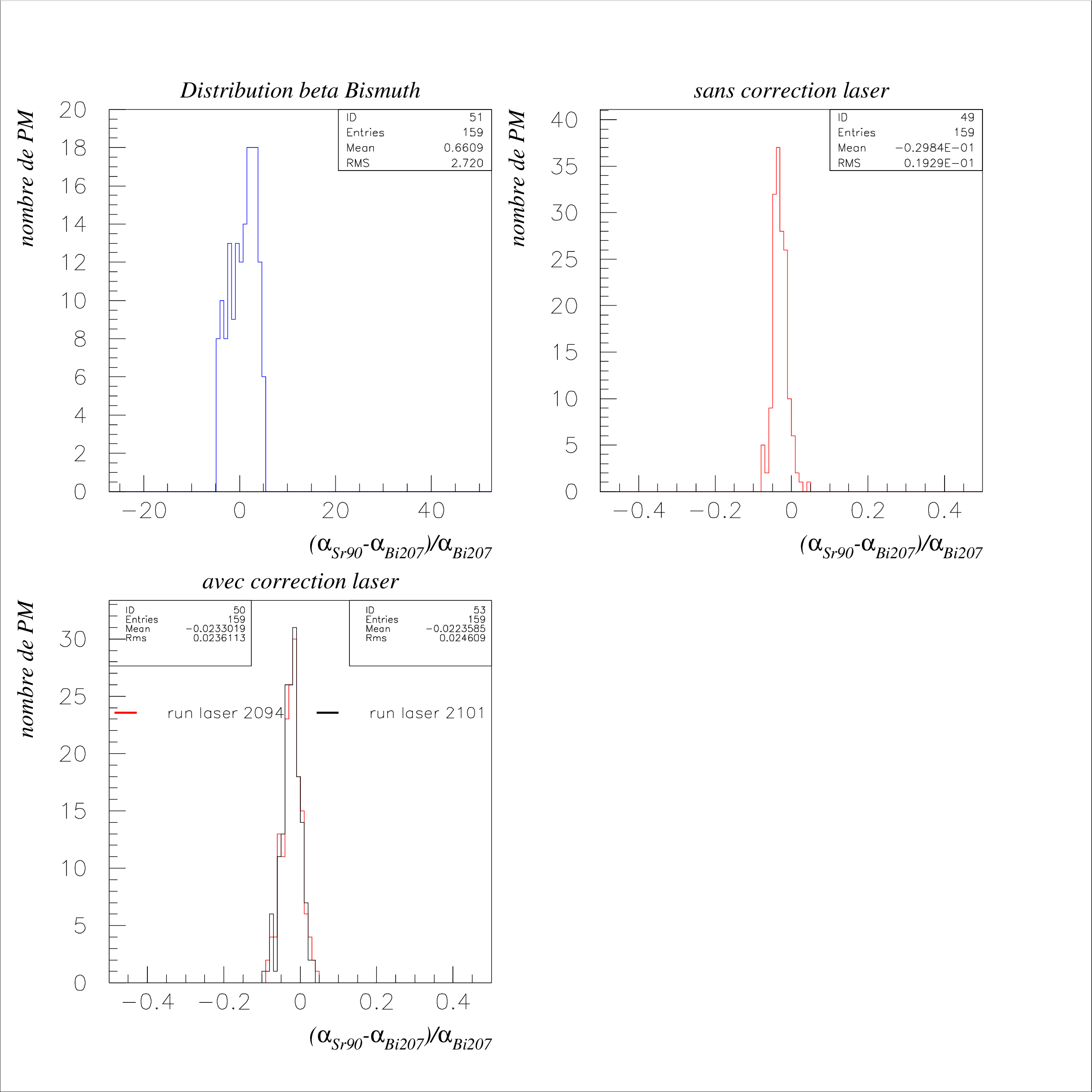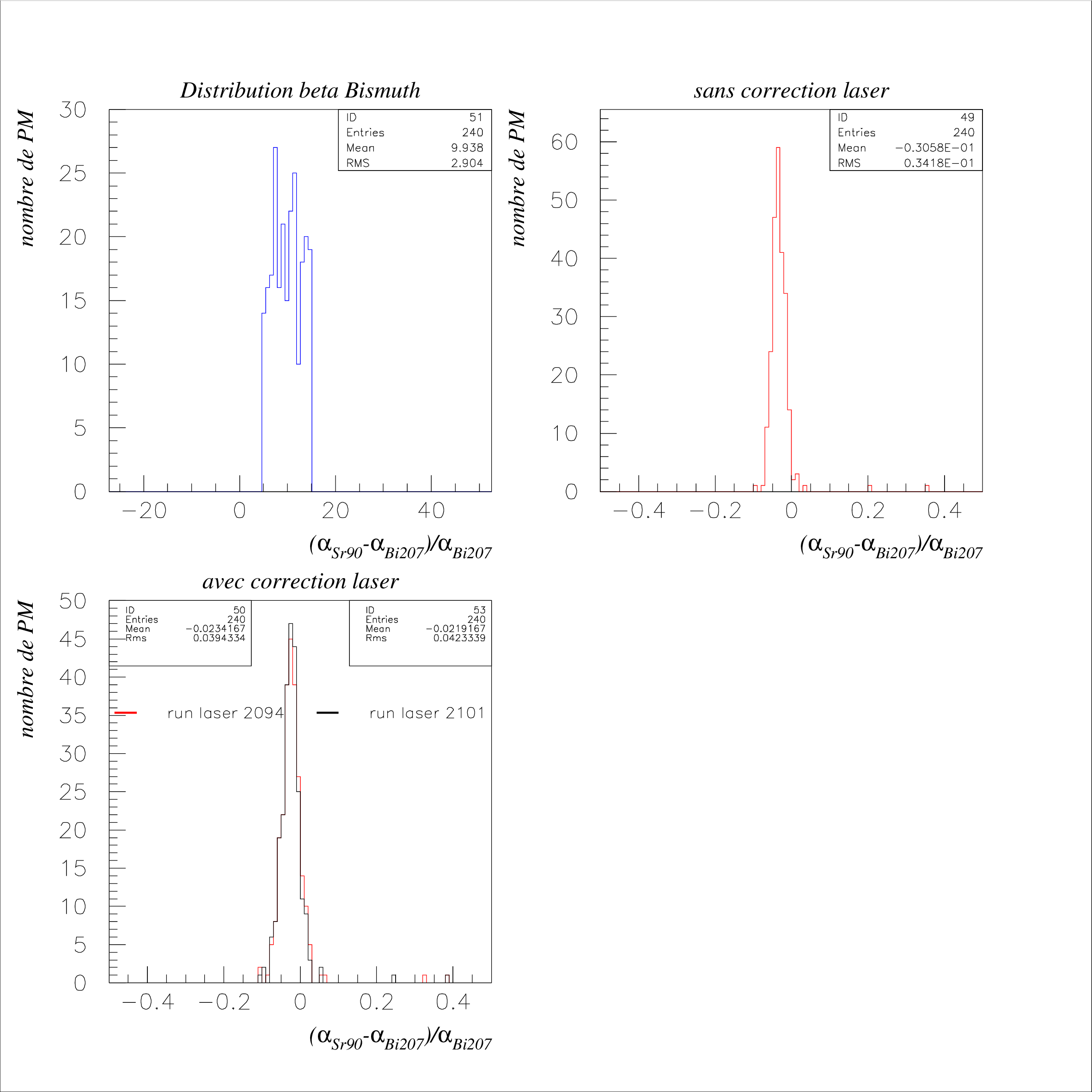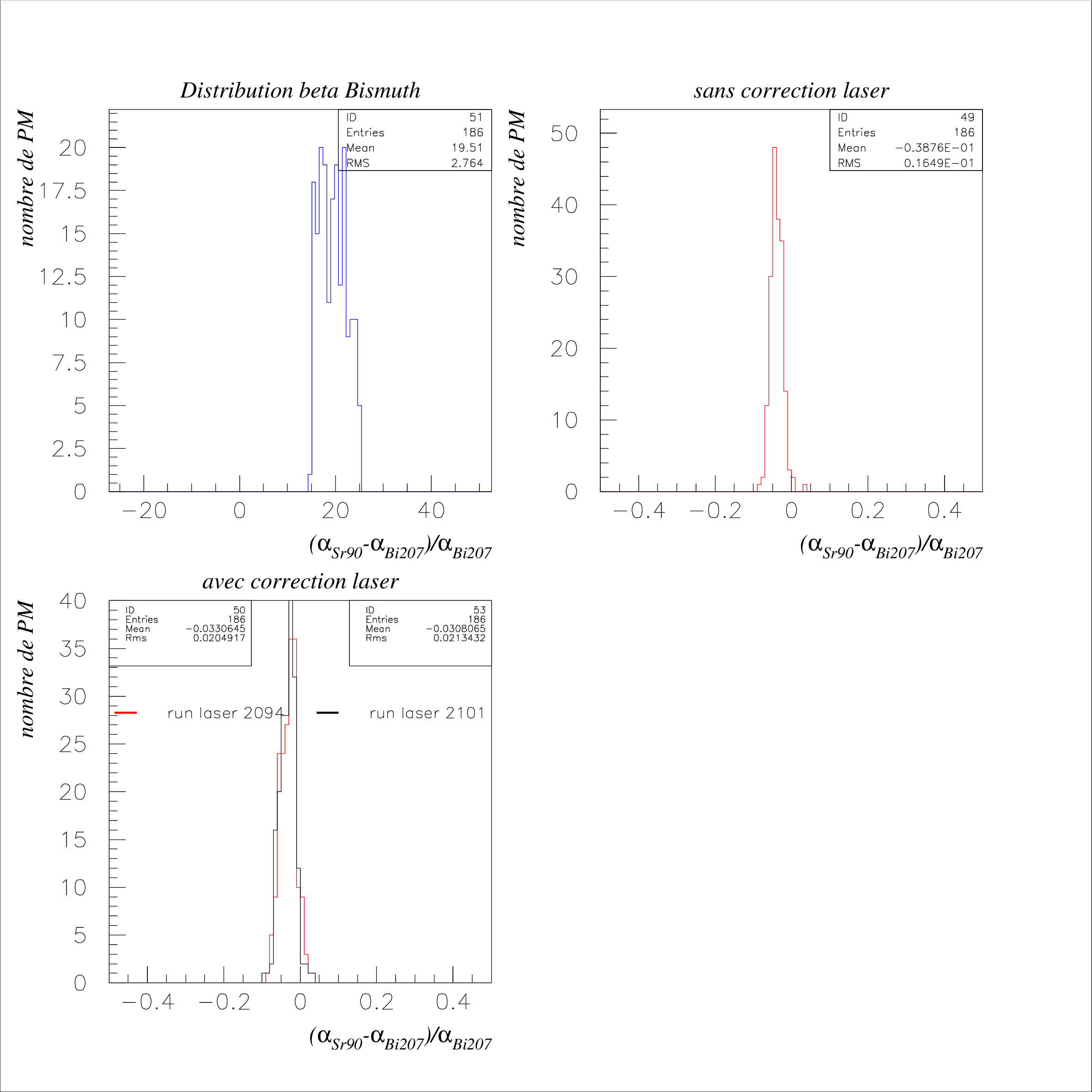

Figure: Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ -5<\beta<5$keV
\includegraphics{save_laser-5+5.eps}

Figure: Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ 5<\beta<15$keV
\includegraphics{save_laser+5+15.eps}

Figure: Comparaison des distribtutions corrigées et non corrigées pour 2 runs de référence $ {}^{207}$Bi: $ 15<\beta<25$keV
\includegraphics{save_laser+15+25.eps}

Cumul des résultats précédents pour la calibration finale

Tous les compteurs n'ont pas pu être calibrés durant cette séance, notamment à cause des problèmes électroniques dont nous avons parlé précédemment. De plus, certains compteurs n'avaient pas assez de statistique pour que l'ajustement des paramètres se fasse dans une barre d'erreur raisonnable.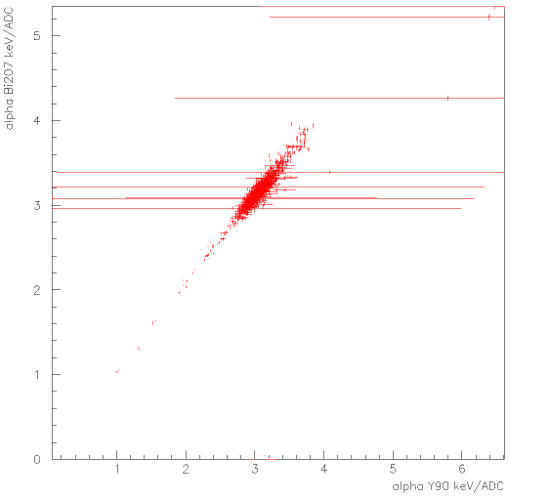
Nous avons dû ainsi identifier dans un premier temps les photomultiplicateurs dont le gain avait, au dessus d'un certain seuil, changé. Nous avons choisi de représenter les coefficients de calibration avec leur barre d'erreur sous forme d'un "diagramme à 2 dimensions" (Fig3.15). Nous pouvons alors facilement identifier graphiquement les photomultiplicateurs situés en dehors de la droite $ y=x$ ou ceux pour lesquels la barre d'erreur est grande. Nous confirmons la variation de gain par les runs lasers correspondants. Si le système laser ne confirme pas cette variation, nous pouvons vérifier la statistique du fit associée au compteur pour repérer une éventuelle erreur dans l'ajustement.

Figure 3.15: Comparaison entre les deux paramètres de calibration $ {}^{90}$Y et $ {}^{207}$Bi: alpha est la pente de la droite de calibrage en keV/canal d'ADC
\includegraphics[width=10cm height=10cm]{compa.eps}

Une fois cette sélection faite, la phase finale de la calibration consiste à synthétiser les paramètres issus du $ {}^{207}$Bi et du $ {}^{90}$Sr. Les sources de $ {}^{106}$Ru ($ Q_{\beta}$=3.540 MeV) n'ont pas été utilisées pour des raisons de temps. Notre choix a été d'ajuster par moindre carrés les trois points de calibration pour chaque compteur (les 2 valeurs corrigées du $ {}^{207}$Bi et la valeur corrigée du $ {}^{90}$Sr). Le fait d'ajuster linéairement suppose que la RMS sur l'énergie varie en $ \sqrt{E}$, hypothèse déjà utilisée dans l'ajustement réalisé sur le $ {}^{90}$Y où la résolution était déduite de celle du $ {}^{207}$Bi pour fiter le spectre. Les 4 paramètres obtenus (pente + offset et leurs erreurs associées) sont alors mis à jour dans la base de données de NEMO jusqu'à la prochaine calibration absolue. La pente moyenne obtenue sur les 1734 photomultiplicateurs ayant pu être calibrés est égale à 3.09 ( $ \sigma=0.23$) keV/canal d'ADC.
Des derniers résultats de simulation semblent indiquer une surestimation de la perte d'énergie de l'électron pour les runs $ {}^{90}$Sr (différence de 50 keV). L'offset obtenu à l'issue du fit sur les 3 points sera alors plus faible étant donné que $ \langle \alpha_{Bi} \rangle> \langle \alpha_{Sr} \rangle$ et que le point du $ {}^{90}$Sr est décalé vers la gauche, ce qui confirme l'idée obtenue avec les corrections lasers sur la non nécessité d'incorporer un offset dans l'ajustement du spectre en forçant la droite de calibrage à passer près du point(0,0)(cf section 3.8).

Conclusion

L'expérience NEMO3 est programmée pour acquérir des données durant de nombreuses années. Il faut donc pouvoir contrôler au mieux la stabilité des compteurs en effectuant régulièrement des tests de calibrage. Cependant, la procédure que nous avons décrite ici est assez lourde et couteuse en temps. En effet, il faut veiller à ne pas détériorer la chambre à fils. C'est pourquoi des runs de longue durée sont nécessaires pour acquérir une statistique suffisante.

Lors de la séance de calibrage effectuée en Avril, des problèmes sur les cartes haute tension n'ont pas permis une stabilisation optimale des photomultiplicateurs, ce qui peut justifier en partie la valeur trouvée pour la résolution à 1 MeV (17 $ \pm$1%).
En utilisant le détecteur de traces avec le $ {}^{207}$Bi, nous avons pu vérifier la capacité du détecteur à sélectionner et à reconstruire les événements cherchés. Les résolutions spatiales obtenues nous donnent une indication sur les coupures à appliquer dans l'algorithme de reconstuction des points d'émission. Cette séance de calibrage n'a pas été optimisée par la présence d'un autre point au dessus de 3 MeV ($ {}^{106}$Ru). Cependant, nos résultats sont validés par la linéarité des photomultiplicateurs jusqu'à 4 MeV. Enfin, les corrections laser nous ont confirmé la validité de la méthode de fit utilisée en mettant en évidence l'indépendance de la correction vis-à-vis de l'offset.

Le détecteur rentre maintenant dans sa phase finale d'assemblage avec la fin de l'installation du blindage à neutrons prévu pour début Juillet 2002. Un nouveau calibrage sera alors effectué pour mettre à jour les paramètres avant le début de l'expérience qui doit durer cinq ans.

Bibliographie

1
K. Errahmane, Thèse à l'université de Paris VII, LAL 01-20 (2001)

2
T. Yanagida, Prog. Theo. Phys. 64 (1980) 1103

3
J. Bonn et al., Nucl. Phys. B, Proc Supp., 91 (2001) 273

4
M. Goeppert Mayer, Phys. Rev. 48 (1935) 512

5
H.V. Klapdor-Kleingrothaus and al., Nuclear Physics A, Volume 694, Issue 1-2, (2001) pp. 269-294.

6
X. Sarazin, "Lasts results on the longitudinal resolution measurement with a laser", Rapport NEMO, Dubna (1998)

7
http://www.hamamatsu.com/

8
C. Marquet, Thèse à l'université de Bordeaux I, No2048 (1999)

9
A. Vareille, Thèse à l'université de Bordeaux I, No1669 (1997)

10
D. Dassie, R. Eschbach, F. Hubert et al.,"NEMO3 Proposal. A proposal for an experiment to study double-beta decay in the search for massive Majorana neutrinos to 0.1 eV", preprint LAL 94-29, Orsay, 1994

11
J. Haas, Calorimètre de NEMO3 et test de photomultiplicateurs (1997)

12
"Table of isotopes", ed. by C.M. Lederer and V.S. Shirley, 7-th ed., John Wiley, New York, 1978

13
R. Arnold et al., The Energy calibration of NEMO3 (1999)

14
NEMO collaboration, Technical design and performance of NEMO3 detector, Technical Report Note (2002)

À propos de ce document...

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

ps : join like me the Cosmology@Home project whose aim is to refine the model that best describes our Universe
    Home | Astronomy | Sciences | Philosophy | Coding | Cv    
- dournac.org © 2003 by fab -

Back to Top