L’expression des lois de la Physique doit être indépendante du système de
coordonnées par rapport auquel ces lois, mises sous forme d’équations, sont
écrites. En ce sens, le calcul tensoriel, appliqué à la Physique, trouve pleinement sa
justification puisqu’il vise précisément à exprimer des propriétés intrinsèques, c’est-à-dire
indépendantes du système de coordonnées utilisé pour les expliciter. On obtient
ainsi des relations qui seules sont susceptibles d’exprimer une certaine réalité
physique.
Par suite, le physicien cherchera à exprimer les propriétés des systèmes physiques sous forme tensorielle. Ceci conduit, éventuellement, à définir et utiliser en Physique de nouvelles entités mathématiques qui soient précisément des tenseurs.
En coordonnées orthogonales ou obliques, les différentielles $\text {d}v_{i}$ des composants covariantes $v_{i}$ d’un vecteur, constituent également les composantes d’un vecteur ; les dérivées partielles $\partial \,v_{i}/\partial \,x^{k}$ forment un tenseur d’ordre deux. Il n’en est plus de même en coordonnées curvilignes quelconques, ainsi que nous l’avons vu au cours de l’exercice (4.10). Examinons les raisons de ces propriétés tensorielles ou non.
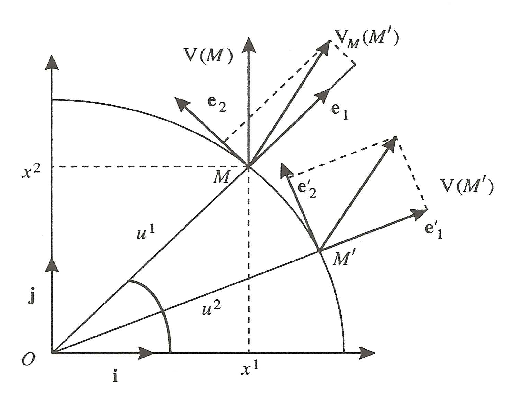
Translation - Pour déterminer la différence entre deux vecteurs $\beq {V}(M)$ et $\beq {V}(M')$ placés
respectivement en deux points $M$ et $M'$ infiniment voisins, il faut au préalable transporter
parallèlement à lui-même le vecteur $\beq {V}(M')$ du point $M'$ au point $M$. Lors de cette translation, ou
transport parallèle, les composantes de $\beq {V}(M')$ ne varient dans le cas de coordonnées
rectilignes (les repères naturels étant identiques en chaque point) et les $\text {d}v_{i}$ sont
évidemment les composantes du vecteur $[\beq {V}(M')-\beq {V}(M)]$.
Par contre, en coordonnées curvilignes, le transport parallèle de $\beq {V}(M')$ au point $M$,
c’est-à-dire sa translation le long d’une droite joignant $M$ à $M'$, va modifier, en
général, la valeur de ses composantes dans le repère naturel. C’est ce que l’on
voit aisément, par exemple, pour un champ de vecteurs en coordonnées polaires
représenté sur la figure(5.1).
Notons $\beq {V_{M}}(M')$ le vecteur $\beq {V}(M')$ transporté parallèlement au point $M$. Le vecteur :
\begin{equation}
\beq{V_{M}}(M’)-\beq{V}(M)=\text{d}\beq{V}
\tag{5.2.2}
\label{5.2.2}
\end{equation}
est appelé la différentielle absolue du vecteur $\mathbf {V}$. Les composantes de $\text {d}\beq {V}$ dans le
repère naturel du point $M$, ne coïncideront pas, en général, avec les différences des
composantes de $\beq {V}(M')$ et $\beq {V}(M)$. Nous allons déterminer l’expression des composantes de
$\text {d}\beq {V}$.
Variation le long d’une géodésique - Nous avons vu que dans l’espace euclidien, les géodésiques sont des droites. Un transport parallèle consiste donc à se déplacer le long d’une géodésique et nous allons étudier les variations d’un vecteur au cours d’un tel déplacement. L’équation des droites, pour un système de coordonnées curvilignes quelconque $y^{i}$ de l’espace ponctuel $\varepsilon _{n}$ est donnée par la relation (5.1.60) :
\begin{equation}
\dfrac{d^{2}\,y^{i}}{\text{d}s^{2}}+\sgammaeq{k}{i}{j}\,\dfrac{\text{d}y^{k}}{\text{d}s}\,\dfrac{\text{d}y^{j}}{\text{d}s}=0
\tag{5.2.3}
\label{5.2.3}
\end{equation}
où $s$ est l’abscisse d’un point de la droite comptée sur celle-ci à partir d’une origine
donnée.
Le vecteur de composantes contravariantes $\text {d}y^{k}/\text {d}s$ est un vecteur unitaire $\mathbf {n}$ porté par la droite ; en d’autres termes, les quantités $\text {d}y^{k}/\text {d}s$ sont les cosinus directeurs de la droite dans chacun des repères naturels $(M,\beq {e_{i}})$. Considérons un vecteur $\mathbf {V}$ de $\varepsilon _{n}$ de composantes covariantes $v_{i}$ et formons le produit scalaire des vecteurs $\mathbf {V}$ et $\mathbf {n}$ ; on a la quantité scalaire suivante :
\begin{equation}
\beq{V}\,\cdot\,\beq{n}=v_{i}\,\dfrac{\text{d}y^{i}}{\text{d}s}
\tag{5.2.4}
\label{5.2.4}
\end{equation}
Lors d’un déplacement le long de la géodésique, d’un point $M$ à un point infiniment voisin $M'$, le scalaire subit la variation :
\begin{equation}
\text{d}\bigg(v_{i}\,\dfrac{\text{d}y^{i}}{\text{d}s}\bigg)=\text{d}v_{k}\,\dfrac{\text{d}y^{k}}{\text{d}s}+v_{i}\,\dfrac{d^{2}\,y^{i}}{\text{d}s^{2}}\,\text{d}s
\tag{5.2.5}
\label{5.2.5}
\end{equation}
Remplaçons dans cette dernière expression, d’une part, la différentielle $\text {d}v_{k}$ par son développement :
\begin{equation}
\text{d}v_{k}=\partial_{j}\,v_{k}\,\dfrac{\text{d}y^{j}}{\text{d}s}\,\text{d}s
\tag{5.2.6}
\label{5.2.6}
\end{equation}
et d’autre part, la dérivée seconde $d^{2}\,y^{i}/\text {d}s^{2}$ par son expression tirée de l’équation des géodésiques (5.2.3). On obtient :
\begin{equation}
\text{d}\bigg(v_{i}\,\dfrac{\text{d}y^{i}}{\text{d}s}\bigg)=(\partial_{j}\,v_{k}-v_{i}\,\sgammaeq{k}{i}{j})\,\dfrac{\text{d}y^{k}}{\text{d}s}\,\dfrac{\text{d}y^{j}}{\text{d}s}\,\text{d}s
\tag{5.2.7}
\label{5.2.7}
\end{equation}
Différentielle absolue - L’expression (5.2.7) peut encore s’écrire :
\begin{equation}
\text{d}(\beq{V}\,\cdot\,\beq{n})=(\partial_{j}\,v_{k}-v_{i}\,\sgammaeq{k}{i}{j})\,\text{d}y^{j}\,\dfrac{\text{d}y^{k}}{\text{d}s}=\text{d}v_{k}\,\dfrac{\text{d}y^{k}}{\text{d}s}
\tag{5.2.8}
\label{5.2.8}
\end{equation}
où l’on a posé :
\begin{equation}
\text{d}v_{k}=(\partial_{j}\,v_{k}-v_{i}\,\sgammaeq{k}{i}{j})\,\text{d}y^{j}
\tag{5.2.9}
\label{5.2.9}
\end{equation}
La variation du produit scalaire $\text {d}(\beq {V}\,\cdot \,\beq {n})$ est égale à la différence des produits scalaires du vecteur $\mathbf {n}$par les vecteurs $\beq {V}(M')$ et $\beq {V}(M)$. Le produit scalaire $\beq {V}(M')\,\cdot \,\beq {n}$ étant indépendant de tout repère, on a :
\begin{equation}
\beq{V}(M’)\,\cdot\,\beq{n}=\beq{V_{M}}(M’)\,\cdot\,\beq{n}
\tag{5.2.10}
\label{5.2.10}
\end{equation}
d’où :
\begin{equation}
\text{d}(\beq{V}\,\cdot\,\beq{n})=\beq{V_{M}}(M’)\,\cdot\,\beq{n}-\beq{V}(M)\,\cdot\,\beq{n}=[\beq{V_{M}}(M’)-\beq{V}(M)]\,\cdot\,\beq{n}=\text{d}\beq{V}\,\cdot\,\beq{n}
\tag{5.2.11}
\label{5.2.11}
\end{equation}
Le vecteur $\text {d}\beq {V}$ est la différentielle absolue du vecteur $\mathbf {V}$, définie par (5.2.2), et il a pour
composantes covariantes, selon la relation (5.2.8), les quantités $\text {d}v_{k}$. Ces dernières
sont appelées les différentielles absolues des composantes covariantes du vecteur
$\mathbf {V}$.
Remarque - En coordonnées curvilignes, la différentiation ordinaire d’un produit dans la formule (5.2.5) peut être utilisée car elle concerne une grandeur scalaire. Par contre, la différentiation ordinaire d’un vecteur $\mathbf {V}$ exprimé dans un repère naturel, $\beq {V}=v^{i}\,\beq {e_{i}}$, ne peut se faire a priori sous la forme classique $\text {d}\beq {V}=v^{i}\,\text {d}\beq {e_{i}}+\text {d}v^{i}\,\beq {e_{i}}$ par suite de la variation des bases naturelles d’un point à un autre. Nous verrons cependant que cette dernière formule s’applique pour la différentielle absolue d’un vecteur.
Composantes covariantes - Les quantités entre parenthèses qui apparaissent dans l’expression (5.2.9) et que l’on note $\nabla _{j}\,v_{k}$, à savoir :
\begin{equation}
\nabla_{j}\,v_{k}=\partial_{j}\,v_{k}-v_{i}\,\sgammaeq{k}{i}{j}
\tag{5.2.12}
\label{5.2.12}
\end{equation}
sont les composantes covariantes d’un tenseur du second ordre ainsi que nous allons le
montrer.
Pour cela, partons des relations de transformation des composantes covariantes d’un vecteur lorsqu’on passe des coordonnées $y^{i}$ aux coordonnées $\bar {y}^{k}$, soit :
\begin{equation}
\bar{v}_{i}=v_{r}\,\dfrac{\partial\,y^{r}}{\partial\,\bar{y}^{i}}=v_{r}\,\partial_{i}\,y^{r}
\tag{5.2.13}
\label{5.2.13}
\end{equation}
où $\bar {v}_{i}$ représente une composante covariante de $\mathbf {V}$ dans le système de coordonnées $\bar {y}^{k}$. La dérivation partielle par rapport à $\bar {y}^{i}$ est notée par le symbole $\partial _{i}$ et l’on a :
\begin{equation}
\partial_{k}\,\bar{v}_{i}=\partial_{k}\,v_{r}\,\partial_{i}\,y^{r}+v_{r}\,\partial_{ki}\,y^{r}
\tag{5.2.14}
\label{5.2.14}
\end{equation}
On a l’expression suivante de la dérivée seconde :
\begin{equation}
\partial_{ki}\,y^{r}=\sgammaeqbar{i}{s}{k}\,\partial_{s}\,y^{r}-\sgammaeq{s}{r}{t}\,\partial_{i}\,y^{s}\,\partial_{k}\,y^{t}
\tag{5.2.15}
\label{5.2.15}
\end{equation}
où les symboles de Christoffel surlignés sont relatifs aux coordonnées $\bar {y}^{k}$.
Démonstration :
\[\begin {array}[b]{lcl} \dfrac {\text {d}^2 y^{r}}{\text {d}s^2} &=& \dfrac {\text {d}}{\text {d}s}\bigg (\dfrac {\text {d} y^{r}}{\text {d}s}\bigg ) = \dfrac {\text {d}}{\text {d}s}\bigg (\dfrac {\partial y^{r}}{\partial \bar {y}^{i}}\dfrac {\text {d}\bar {y}^{i}}{\text {d}s}\bigg ) = \dfrac {\text {d}}{\text {d}s}\bigg (\dfrac {\partial y^{r}}{\partial \bar {y}^{i}}\bigg )\dfrac {\text {d}\bar {y}^{i}}{\text {d}s} + \dfrac {\partial y^{r}}{\partial \bar {y}^{i}} \dfrac {\text {d}^2\bar {y}^{i}}{\text {d}s^2} \\[2ex] &=& \dfrac {1}{\text {d}s} \dfrac {\partial }{\partial \bar {y}^{k}} \bigg (\dfrac {\partial y^{r}}{\partial \bar {y}^{i}}\bigg ) \text {d}\bar {y}^{k} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} + \dfrac {\partial y^{r}}{\partial \bar {y}^{i}} \dfrac {\text {d}^2\bar {y}^{i}}{\text {d}s^2} \\[2ex] &=& \dfrac {\partial }{\partial \bar {y}^{k}} \bigg (\dfrac {\partial y^{r}}{\partial \bar {y}^{i}}\bigg ) \dfrac {\text {d}\bar {y}^{k}}{\text {d}s} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} - \dfrac {\partial y^{r}}{\partial \bar {y}^{s}} \sgammaeqbar {i}{s}{k} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} \dfrac {\text {d}\bar {y}^{k}}{\text {d}s} \\[2ex] &=& -\sgammaeq {s}{r}{t} \dfrac {\text {d}y^{s}}{\text {d}s} \dfrac {\text {d}y^{t}}{\text {d}s} \\[2ex] &=& -\sgammaeq {s}{r}{t} \dfrac {\partial y^{s}}{\partial \bar {y}^{i}} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} \dfrac {\partial y^{t}}{\partial \bar {y}^{k}} \dfrac {\text {d}\bar {y}^{k}}{\text {d}s} = -\sgammaeq {s}{r}{t}\, \partial _{i}\, y^{s} \partial _{k}\, y^{t}\, \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} \dfrac {\text {d}\bar {y}^{k}}{\text {d}s} \\[2ex] &=& \partial _{ki}\,y^{r}\,\dfrac {\text {d}\bar {y}^{k}}{\text {d}s} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} - \partial _{s}\,y^{r}\,\sgammaeqbar {i}{s}{k} \dfrac {\text {d}\bar {y}^{k}}{\text {d}s} \dfrac {\text {d}\bar {y}^{i}}{\text {d}s} \\[2ex] &\Longrightarrow &\, \partial _{ki}\,y^{r} = \sgammaeqbar {i}{s}{k}\,\partial _{s}\,y^{r} - \sgammaeq {s}{r}{t}\,\partial _{i}\,y^{s}\,\partial _{k}\,y^{t} \end {array}\]
La relation (5.2.14) peut alors s’écrire :
\begin{equation}
\partial_{k}\,\bar{v}_{i}=\dfrac{\partial\,v_{r}}{\partial\,y^{s}}\,\partial_{i}\,y^{r}\,\partial_{k}\,y^{s}+\sgammaeqbar{i}{t}{k}\,\bar{v}_{t}-\sgammaeq{r}{t}{s}\,v_{t}\,\partial_{i}\,y^{r}\,\partial_{k}\,y^{s}
\tag{5.2.16}
\label{5.2.16}
\end{equation}
Cette dernière expression peut être réarrangée sous la forme suivante :
\begin{equation}
\dfrac{\partial\,\bar{v}_{i}}{\partial\,\bar{y}^{k}}-\sgammaeqbar{i}{t}{k}\,\bar{v}_{t}=\bigg(\dfrac{\partial\,v_{r}}{\partial\,y^{s}}-\sgammaeq{r}{t}{s}\,v_{t}\bigg)\,\partial_{i}\,y^{r}\,\partial_{k}\,y^{s}
\tag{5.2.17}
\label{5.2.17}
\end{equation}
Cette relation, vérifiant la loi de changement de coordonnées des composantes
covariantes d’un tenseur d’ordre deux, montre que les quantités $\nabla _{j}\,v_{k}$ sont les
composantes covariantes d’un tenseur d’ordre deux qui est appelé la dérivée
covariante du vecteur $\mathbf {V}$.
Champ uniforme - Si toutes composantes $\nabla _{j}\,v_{k}$ de la dérivée covariante sont nulles, les
variations du produit scalaire $\beq {V}\,\cdot \,\beq {n}$ sont nulles et par suite les différents vecteurs du champ
sont équipollents entre eux. On est en présence d’un champ uniforme.
On remarque que, dans ce cas, les dérivées partielles $\partial _{j}\,v_{k}$ ne sont pas nulles et qu’il en est
de même pour la diffŕentielle $\text {d}v_{k}$. Ceci résulte du fait que les repères naturels, pour un
système de coordonnées curvilignes quelconque, ne sont pas identiques en chaque
point.
L’égalité par translation de deux vecteurs se traduit par le fait que le tenseur dérivée
covariante doit être identiquement nul pour cette translation.
Composantes mixtes - Les composantes mixtes du tenseur dérivée covariante sont données par :
\begin{equation}
g^{ik}\,\nabla_{j}\,v_{k}=g^{ik}\,(\partial_{j}\,v_{k}-v_{r}\,\sgammaeq{k}{r}{j})
\tag{5.2.18}
\label{5.2.18}
\end{equation}
Remplaçons dans l’expression précďente le terme $g^{ik}\,\partial _{j}\,v_{k}$ tiré de la relation suivante :
\begin{equation}
\partial_{j}\,(g^{ik}\,v_{k})=v_{k}\,\partial_{j}\,g^{ik}+g^{ik}\,\partial_{j}\,v_{k}=\partial_{j}\,v^{i}
\tag{5.2.19}
\label{5.2.19}
\end{equation}
et utilisant l’expression suivante obtenue à partir des relations (5.1.19) et (5.1.28) :
\begin{equation}
\partial_{j}\,g^{ik}=-g^{il}\,\sgammaeq{j}{k}{l}-g^{kl}\,\sgammaeq{j}{i}{l}
\tag{5.2.20}
\label{5.2.20}
\end{equation}
on obtient :
\begin{equation}
g^{ik}\,\nabla_{j}\,v_{k}=\partial_{j}\,v^{i}-v_{k}\,\partial_{j}\,g^{ik}-g^{ik}\,v_{r}\,\sgammaeq{k}{r}{j}=\partial_{j}\,v^{i}+v_{k}\,g^{kl}\,\sgammaeq{j}{i}{l}
\tag{5.2.21}
\label{5.2.21}
\end{equation}
Les deux derniers termes de l’équation précédente font apparaître les composantes contravariantes $v^{l}$ du vecteur $\mathbf {V}$. Les composantes mixtes du tenseur dérivée covariante, notées $\nabla _{j}\,v^{i}$, sont donc données par :
\begin{equation}
\nabla_{j}\,v^{i}=\partial_{j}\,v^{i}+v^{l}\,\sgammaeq{j}{i}{l}
\tag{5.2.22}
\label{5.2.22}
\end{equation}
Linéarité de la dérivée covariante - Considérons le vecteur $\beq {T}=\beq {U}+\beq {V}$ de composantes contravariantes $t^{k}=u^{k}+v^{k}$ ; sa dérivée covariante est donnée par :
\begin{equation}
\begin{array}[b]{lcl}
\nabla_{j}\,t^{k}&=&\partial_{j}\,t^{k}+\sgammaeq{i}{k}{j}\,t^{i}=\partial_{j}\,(u^{k}+v^{k})+\sgammaeq{i}{k}{j}\,(u^{i}+v^{i}) \\
&=&(\partial_{j}\,u^{k}+\sgammaeq{i}{k}{j}\,u^{i})+(\partial_{j}\,v^{k}+\sgammaeq{i}{k}{j}\,v^{i})
\end{array}
\tag{5.2.23}
\label{5.2.23}
\end{equation}
On voit apparaître les dérivées covariantes des vecteurs $\mathbf {U}$ et $\mathbf {V}$, d’où :
\begin{equation}
\nabla_{j}\,t^{k}=\nabla_{j}\,u^{k}+\nabla_{j}\,v^{k}
\tag{5.2.24}
\label{5.2.24}
\end{equation}
La dérivée covariante d’une somme de vecteurs est égale à la somme des dérivées covariantes. On obtient de même pour un vecteur $\beq {T}=\lambda \,\beq {U}$, où $\lambda $ est une constante :
\begin{equation}
\nabla_{j}\,(\lambda\,u^{k})=\lambda\,\nabla_{j}\,u^{k}
\tag{5.2.25}
\label{5.2.25}
\end{equation}
Les calculs et définitions précédentes s’étendent sans difficulté à des tenseurs d’ordre
quelconque. Montrons le sur un exemple en considérant les composantes $u^{r}_{st}$ d’un tenseur du
troisième ordre.
Choisissons pour cela trois champs de vecteurs uniformes de composantes respectives $a_{r}$, $b^{s}$, $c^{t}$ et formons le produit contracté $u^{r}_{st}\,a_{r}\,b^{s}\,c^{t}$. On obtient un scalaire dont la variation élémentaire s’écrit :
\begin{equation}
\begin{array}[b]{lcl}
\text{d}(u^{r}_{st}\,a_{r}\,b^{s}\,c^{t})&=&(\partial_{k}\,u^{r}_{st}\,a_{r}\,b^{s}\,c^{t}+u^{r}_{st}\,\partial_{k}\,a_{r}\,b^{s}\,c^{t}\\
&+&u^{r}_{st}\,a_{r}\,\partial_{k}\,b^{s}\,c^{t}+u^{r}_{st}\,a_{r}\,b^{s}\,\partial_{k}\,c^{t})\,\text{d}y^{k}
\end{array}
\tag{5.2.26}
\label{5.2.26}
\end{equation}
Les champs de vecteurs $a_{r}$, $b^{s}$, $c^{t}$ étant uniformes, les dérivées covariantes de leurs composantes sont nulles et l’on obtient donc pour expression de leurs dérivées partielles :
\begin{equation}
\partial_{k}\,a_{r}=a_{i}\,\sgammaeq{k}{i}{r}\,\,\,;\,\,\,\partial_{k}\,b^{s}=-b^{i}\,\sgammaeq{i}{s}{k}\,\,\,;\,\,\,\partial_{k}\,c^{t}=-c^{i}\,\sgammaeq{i}{t}{k}
\tag{5.2.27}
\label{5.2.27}
\end{equation}
Reportant ces expressions dans la relation (5.2.26) donnant la variation élémentaire, il vient :
\begin{equation}
\text{d}(u^{r}_{st}\,a_{r}\,b^{s}\,c^{t})=(\partial_{k}\,u^{r}_{st}+u^{i}_{st}\,\sgammaeq{k}{r}{i}-u^{r}_{it}\,\sgammaeq{k}{i}{s}-u^{r}_{si}\,\sgammaeq{k}{i}{t})\,a_{r}\,b^{s}\,c^{t}\,\text{d}y^{k}
\tag{5.2.28}
\label{5.2.28}
\end{equation}
Cette relation met en évidence le système tensoriel suivant :
\begin{equation}
\nabla_{k}\,u^{r}_{st}=\partial_{k}\,u^{r}_{st}+u^{i}_{st}\,\sgammaeq{k}{r}{i}-u^{r}_{it}\,\sgammaeq{k}{i}{s}-u^{r}_{si}\,\sgammaeq{k}{i}{t}
\tag{5.2.29}
\label{5.2.29}
\end{equation}
qui généralise les expressions de la dérivée covariante d’un vecteur. Par définition, les
quantités $\nabla _{k}\,u^{r}_{st}$ sont les dérivées covariantes des composantes mixtes $u^{r}_{st}$ du tenseur
$\mathbf {U}$.
On voit apparaître dans cette expression la règle de formation de la dérivée
covariante des composantes d’un tenseur d’ordre quelconque. À la dérivée partielle
classique d’une composante, dans le cas $u^{r}_{st}$, s’ajoute un terme de la forme $u^{i}_{st}\,\sgammaeq {k}{r}{i}$ pour
chaque indice contravariant et se retranche un terme de la forme $u^{r}_{it}\,\sgammaeq {k}{i}{s}$ pour chaque
indice covariant, la sommation dans chacun de ces termes s’effectuant sur l’indice
considéré.
La dérivation covariante se réduit à la dérivation partielle ordinaire pour un système
de coordonnées cartésiennes.
On démontre la propriété de tensorialité de la dérivée covariante des composantes d’un tenseur de façon analogue à celle déjà utilisée pour la dérivée covariante des composantes d’un tenseur.
Linéarité - Les propriétés de linéarité de la dérivée covariante des composantes d’un tenseur résulte de la linéarité de la dérivée partielle et celles des termes supplémentaires. On a par exemple, pour un tenseur $w^{r}_{st}=u^{r}_{st}+v^{r}_{st}$ :
\begin{equation}
\nabla_{k}\,w^{r}_{st}=\nabla_{k}\,u^{r}_{st}+\nabla_{k}\,v^{r}_{st}
\tag{5.2.30}
\label{5.2.30}
\end{equation}
\begin{equation}
\nabla_{k}\,(\lambda\,u^{r}_{st})=\lambda\,\nabla_{k}\,u^{r}_{st}
\tag{5.2.31}
\label{5.2.31}
\end{equation}
Dérivée covariante d’un produit tensoriel - Considérons par exemple le produit tensoriel suivant :
\begin{equation}
w^{r}_{st}=u^{r}_{s}\,v_{t}
\tag{5.2.32}
\label{5.2.32}
\end{equation}
La dérivée covariante de ce produit tensoriel s’écrit :
\begin{equation}
\nabla_{k}\,w^{r}_{st}=\nabla_{k}\,(u^{r}_{s}\,v_{t})=(\partial_{k}\,u^{r}_{s}+u^{i}_{s}\,\sgammaeq{k}{r}{i}-u^{r}_{i}\,\sgammaeq{k}{i}{s})\,v_{t}+(\partial_{k}\,v_{t}-v_{i}\,\sgammaeq{t}{i}{k})\,u^{r}_{s}
\tag{5.2.33}
\label{5.2.33}
\end{equation}
On voit apparaître les dérivées covariantes de chacun des tenseurs $u^{r}_{s}$ et $v_{t}$ ; on a donc la relation :
\begin{equation}
\nabla_{k}\,(u^{r}_{s}\,v_{t})=v_{t}\,\nabla_{k}\,u^{r}_{s}+u^{r}_{s}\,\nabla_{k}\,v_{t}
\tag{5.2.34}
\label{5.2.34}
\end{equation}
On obtient pour la dérivée covariante du produit tensoriel une règle de dérivation
analogue à celle de la dérivée partielle ordinaire du produit de deux fonctions.
Contraction - La dérivation covariante et la contraction sont deux opérations permutables. Montrons cette propriété par exemple sur le tenseur $u^{r}_{st}$. La dérivée covariante de ce tenseur est donnée par la relation (5.2.29), à savoir :
\begin{equation}
\nabla_{k}\,u^{r}_{st}=\partial_{k}\,u^{r}_{st}+u^{i}_{st}\,\sgammaeq{k}{r}{i}-u^{r}_{it}\,\sgammaeq{k}{i}{s}-u^{r}_{si}\,\sgammaeq{k}{i}{t}
\tag{5.2.35}
\label{5.2.35}
\end{equation}
Effectuons une contraction sur les indices $r$ et $t$ en faisant $t=r$ ; ceci revient à calculer les
quantités $\delta ^{t}_{r}\,\nabla _{k}\,u^{r}_{st}$.
Après contraction, dans le second membre de la relation (5.2.35), le deuxième et le quatrième terme, qui ne diffèrent que par les noms des indices muets, sont identiques et ils s’annulent ; la relation (5.2.35) se réduit alors à :
\begin{equation}
\nabla_{k}\,u^{r}_{sr}=\partial_{k}\,u^{r}_{sr}-u^{r}_{ir}\,\sgammaeq{k}{i}{s}
\tag{5.2.36}
\label{5.2.36}
\end{equation}
On obtient une expression identique en contractant d’abord les composantes, soit $u^{r}_{sr}=\delta ^{t}_{r}\,u^{r}_{st}$, puis en calculant la dérivée covariante $\nabla _{k}\,u^{r}_{sr}$ des composantes contractées. On a donc :
\begin{equation}
\delta^{t}_{r}(\nabla_{k}\,u^{r}_{st})=\nabla_{k}\,(\delta^{t}_{r}\,u^{r}_{st})
\tag{5.2.37}
\label{5.2.37}
\end{equation}
La contraction et la dérivation covariante sont donc des opérations
permutables.
Produit contracté - On va en déduire que la règle (5.2.34) de dérivation covariante du
produit tensoriel peut s’appliquer à un produit contracté.
Soit par exemple, les composantes d’un tenseur formées par le produit contracté $u^{ij}_{k}\,v_{mi}$. Utilisons la propriété de permutation (5.2.37) ainsi que la règle de dérivation covariante (5.2.34) ; on obtient :
\begin{equation}
\begin{array}[b]{lcl}
\nabla_{r}\,(u^{ij}_{k}\,v_{mi})&=&\delta^{q}_{i}\,\nabla_{r}\,(u^{ij}_{k}\,v_{mq})=\delta^{q}_{i}\,(\nabla_{r}\,u^{ij}_{k})\,v_{mq}+\delta^{q}_{i}\,u^{ij}_{k}\,(\nabla_{r}\,v_{mq})\\
&=&(\nabla_{r}\,u^{ij}_{k})\,v_{mi}+u^{ij}_{k}\,(\nabla_{r}\,v_{mi})
\end{array}
\tag{5.2.38}
\label{5.2.38}
\end{equation}
Considérons un vecteur $\mathbf {V}$ de composantes covariantes $v_{i}$. Les quantités données par (5.2.12), à savoir :
\begin{equation}
\nabla_{j}\,v_{i}=\partial_{j}\,v_{i}-v_{l}\,\sgammaeq{j}{l}{i}
\tag{5.2.39}
\label{5.2.39}
\end{equation}
sont les composantes covariantes de la dérivée covariante du vecteur $\mathbf {V}$. Calculons la
dérivée covariante seconde de ce vecteur, par rapport à une coordonnée curviligne
$y^{k}$.
Appliquons la règle de formation de la dérivée covariante d’un tenseur aux composantes covariantes $\nabla _{j}\,v_{i}$, il vient :
\begin{equation}
\nabla_{k}(\nabla_{j}\,v_{i})=\partial_{k}\,(\nabla_{j}\,v_{i})-\sgammaeq{i}{r}{k}\,(\nabla_{j}\,v_{r})-\sgammaeq{j}{r}{k}\,(\nabla_{r}\,v_{i})
\tag{5.2.40}
\label{5.2.40}
\end{equation}
Substituant l’expression (5.2.39) dans la relation précédente, on obtient :
\begin{equation}
\begin{array}[b]{lcl}
\nabla_{k}(\nabla_{j}\,v_{i})&=&\partial_{kj}\,v_{i}-(\partial_{k}\,\sgammaeq{j}{l}{i})\,v_{l}-\sgammaeq{j}{l}{i}\,\partial_{k}\,v_{l}\\
& & \\
& &-\sgammaeq{i}{r}{k}\,\partial_{j}\,v_{r}+\sgammaeq{i}{r}{k}\,\sgammaeq{j}{l}{r}\,v_{l}-\sgammaeq{j}{r}{k}\,\partial_{r}\,v_{i}+\sgammaeq{j}{r}{k}\,\sgammaeq{r}{l}{i}\,v_{l}
\end{array}
\tag{5.2.41}
\label{5.2.41}
\end{equation}